机器学习-分类问题B

数学公式在渲染器中会出现错误，目前还没有解决

Outline

  1. Nonlinear classifiers
  2. Kernel trick and kernel SVM
  3. Ensemble Methods - Boosting, Random Forests
  4. Classification Summary
1
2
3
4
5
6
7
8
9
10
# setup
%matplotlib inline
import matplotlib_inline   # setup output image format
matplotlib_inline.backend_inline.set_matplotlib_formats('retina')
import matplotlib.pyplot as plt
plt.rcParams['figure.dpi'] = 100  # display larger images
import matplotlib
from numpy import *
from sklearn import *
from scipy import stats
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
def drawstump(fdim, fthresh, fdir='gt', poscol=None, negcol=None, lw=2, ls='k-'):
    # fdim = dimension
    # fthresh = threshold
    # fdir = direction (gt, lt)
    
    if fdir == 'lt':
        # swap colors
        tmp = poscol
        poscol = negcol
        negcol = tmp
    
    # assume fdim=0
    polyxn = [fthresh, fthresh, -30, -30]
    polyyn = [30, -30, -30, 30]
    
    polyxp = [fthresh, fthresh, 30, 30]
    polyyp = [30, -30, -30, 30]
        
    # fill positive half-space or neg space
    if (poscol):
        if fdim==0:
            plt.fill(polyxp, polyyp, poscol, alpha=0.2)
        else:
            plt.fill(polyyp, polyxp, poscol, alpha=0.2)            
    
    if (negcol):
        if fdim==0:
            plt.fill(polyxn, polyyn, negcol, alpha=0.2)
        else:
            plt.fill(polyyn, polyxn, negcol, alpha=0.2)

    # plot line
    if fdim==0:
        plt.plot(polyxp[0:2], polyyp[0:2], ls, lw=lw)
    else:
        plt.plot(polyyp[0:2], polyxp[0:2], ls, lw=lw)

def drawplane(w, b=None, c=None, wlabel=None, poscol=None, negcol=None, lw=2, ls='k-'):
    # w^Tx + b = 0
    # w0 x0 + w1 x1 + b = 0
    # x1 = -w0/w1 x0 - b / w1

    # OR
    # w^T (x-c) = 0 = w^Tx - w^Tc  --> b = -w^Tc
    if c != None:
        b = -sum(w*c)
    
    # the line
    if (abs(w[0])>abs(w[1])):   # vertical line
        x0 = array([-30,30])
        x1 = -w[0]/w[1] * x0 - b / w[1]
    else:                       # horizontal line
        x1 = array([-30,30])
        x0 = -w[1]/w[0] * x1 - b / w[0]
    
    # fill positive half-space or neg space
    if (poscol):
        polyx = [x0[0], x0[-1], x0[-1], x0[0]]
        polyy = [x1[0], x1[-1], x1[0], x1[0]]
        plt.fill(polyx, polyy, poscol, alpha=0.2)
    
    if (negcol):
        polyx = [x0[0], x0[-1], x0[0], x0[0]]
        polyy = [x1[0], x1[-1], x1[-1], x1[0]]
        plt.fill(polyx, polyy, negcol, alpha=0.2)
        
    # plot line
    lineplt, = plt.plot(x0, x1, ls, lw=lw)

    # the w
    if (wlabel):
        xp = array([0, -b/w[1]])
        xpw = xp+w
        plt.arrow(xp[0], xp[1], w[0], w[1], width=0.01)
        plt.text(xpw[0]-0.5, xpw[1], wlabel)
    return lineplt

Ensemble Classifiers

  • Why trust only one expert?

    • In real life, we may consult several experts, or go with the “wisdom of the crowd”
    • In machine learning, why trust only one classifier?

  • Ensemble methods aim to combine multiple classifiers together to form a better classifier.

  • Examples:

    • boosting - training multiple classifiers, each focusing on errors made by previous classifiers.
    • bagging - training multiple classifiers from random selection of training data

AdaBoost - Adaptive Boosting

  • Base classifier is a “weak learner”
    • A simple classifier that can be slightly better than random chance (>50%)
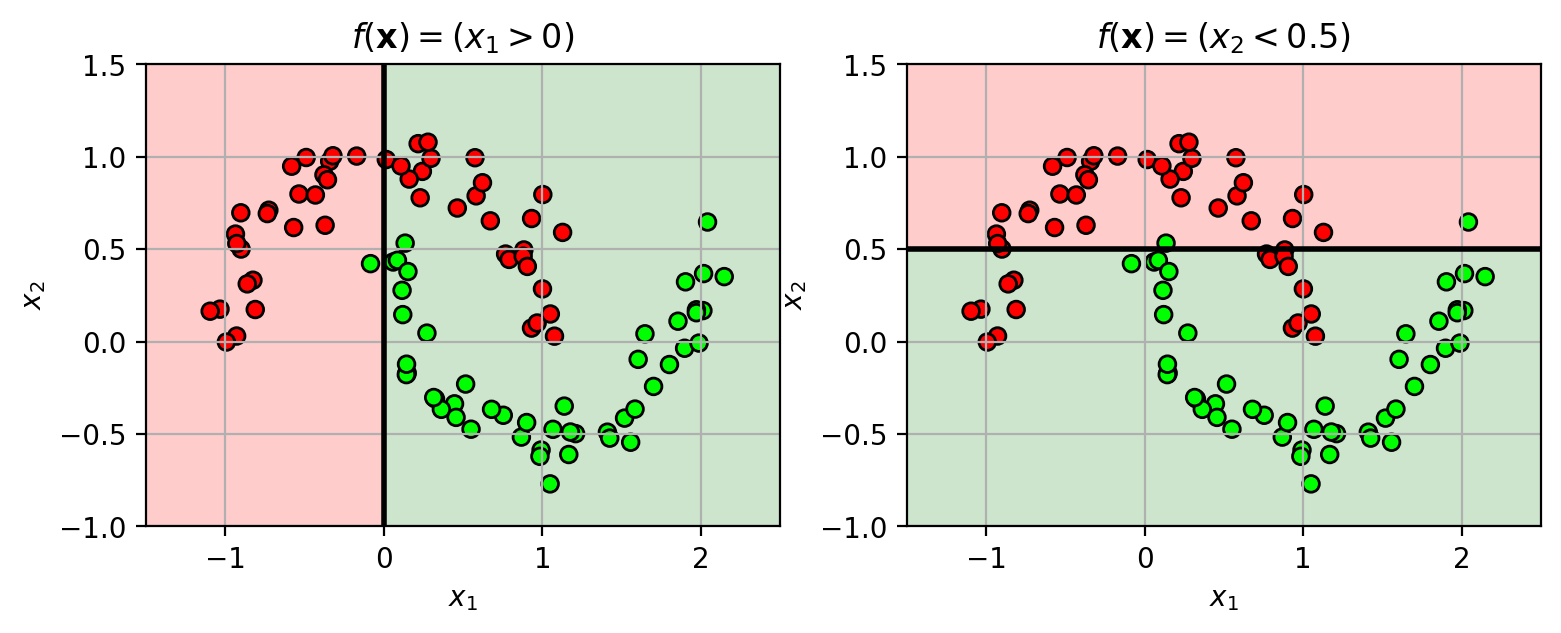
    • Example: decision stump classifier
      • check if feature value is above (or below) a threshold.
      • $y = h(x) = \begin{cases}+1, & x_j \geq T \ -1, & x_j\lt T \end{cases}$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# type three - moons
from sklearn import datasets

X3,Y3 = datasets.make_moons(n_samples=100,
                                             noise=0.1, random_state=4487)
mycmap = matplotlib.colors.LinearSegmentedColormap.from_list('mycmap', ["#FF0000", "#FFFFFF", "#00FF00"])

axbox3 = [-1.5, 2.5, -1, 1.5]

wlfig = plt.figure(figsize=(9,3))
plt.subplot(1,2,1)
drawstump(0, 0, poscol='g', negcol='r')
plt.scatter(X3[:,0], X3[:,1], c=Y3, cmap=mycmap, edgecolors='k')
plt.xlabel('$x_1$'); plt.ylabel('$x_2$'); plt.grid(True)
plt.axis(axbox3)
plt.title('$f(\mathbf{x}) = (x_1>0)$')

plt.subplot(1,2,2)
drawstump(1, 0.5, fdir='lt', poscol='g', negcol='r')
plt.scatter(X3[:,0], X3[:,1], c=Y3, cmap=mycmap, edgecolors='k')
plt.xlabel('$x_1$'); plt.ylabel('$x_2$'); plt.grid(True)
plt.axis(axbox3)
plt.title('$f(\mathbf{x}) = (x_2<0.5)$')
plt.close()
1
wlfig

png

  • Idea: train weak classifiers sequentially
  • In each iteration,
    • Pick a weak learner $h_t(\mathbf{x})$ that best carves out the input space.
    • The weak learner should focus on data that is misclassified.
      • Apply weights to each sample in the training data.
      • Higher weights give more priority to difficult samples.
    • Combine all the weak learners into a strong classifier: $f_t(\mathbf{x}) = f_{t-1}(\mathbf{x}) + \alpha_t h_t(\mathbf{x})$
      • $\alpha_t$ is a weight for each weak learner.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
def plot_boosting(model, axbox, X):

    # grid points
    xr = [ linspace(axbox[0], axbox[1], 200), 
           linspace(axbox[2], axbox[3], 200) ]

    # make a grid for calculating the posterior, 
    #  then form into a big [N,2] matrix
    xgrid0, xgrid1 = meshgrid(xr[0], xr[1])
    allpts = c_[xgrid0.ravel(), xgrid1.ravel()]

    # calculate the decision function
    if hasattr(model, 'decision_function'):
        score = model.decision_function(allpts).reshape(xgrid0.shape)
    else:
        score = model.predict_proba(allpts)[:,1].reshape(xgrid0.shape)  
        # pass through a logit
        score = log(score / (1-score))
    maxscore = ceil(abs(score).max())
    mylevels = linspace(-maxscore, maxscore, 11)

    plt.imshow(score, origin='lower', extent=axbox, alpha=0.30, cmap=mycmap, 
               vmin=-maxscore, vmax=maxscore, aspect='auto')

    #plt.contourf(xr[0], xr[1], score, levels=mylevels, cmap=mycmap, alpha=0.3)
    plt.contour(xr[0], xr[1], score, levels=[0], linestyles='solid', colors='k',
                linewidths=2)
    
    plt.axis(axbox); plt.grid(True)    
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
plts = {}
ns = [1, 2, 3, 4, 5]
N = X3.shape[0]
XW = ones(N) / N
from sklearn import ensemble

for n in ns:
    # run the discrete Boosting algorithm
    clf = ensemble.AdaBoostClassifier(n_estimators=n, random_state=4487, algorithm='SAMME')
    clf.fit(X3, Y3)

    plts[n] = plt.figure(figsize=(9,3))
    
    # show the weak learner
    wl = clf.estimators_[n-1]
    wlf = wl.tree_.feature[0]
    wlt = wl.tree_.threshold[0]

    if wl.tree_.value[2,0,1] > wl.tree_.value[2,0,0]:
        wld = 'gt'
    else:
        wld = 'lt'
    
    plt.subplot(1,2,1)
    drawstump(wlf, wlt, fdir=wld, poscol='g', negcol='r')
    mys = 20*sqrt(XW*N)
    plt.scatter(X3[:,0], X3[:,1], c=Y3, s=mys, cmap=mycmap, edgecolors='k')
    plt.xlabel('$x_1$'); plt.ylabel('$x_2$')
    plt.axis(axbox3); plt.grid(True)
    plt.title('iter '+str(n) + " weak learner")

    plt.subplot(1,2,2)
    plot_boosting(clf, axbox3, X3)
    plt.scatter(X3[:,0], X3[:,1], c=Y3, cmap=mycmap, edgecolors='k')

    plt.xlabel('$x_1$'); plt.ylabel('$x_2$')
    plt.title('iter '+str(n) + " classifier")
        
    # calculate updated weights (for AdaBoost)
    # can't find these in the sklearn version
    tmpY = clf.estimators_[n-1].predict(X3)
    err = sum((tmpY != Y3)*XW)
    alpha = 0.5*log((1-err) / err)
    scale = 2*(tmpY!=Y3)-1
    XW = XW * exp(scale*alpha)
    XW = XW / sum(XW)
    plt.close()

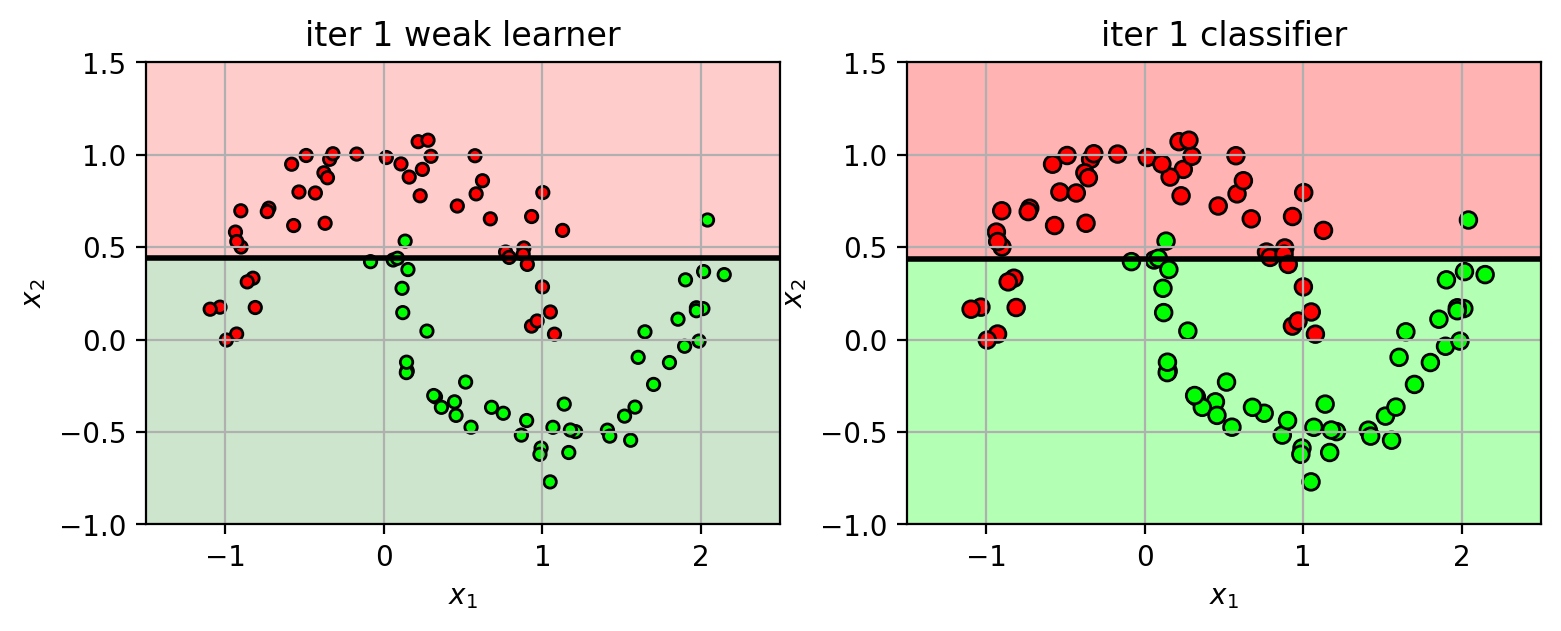
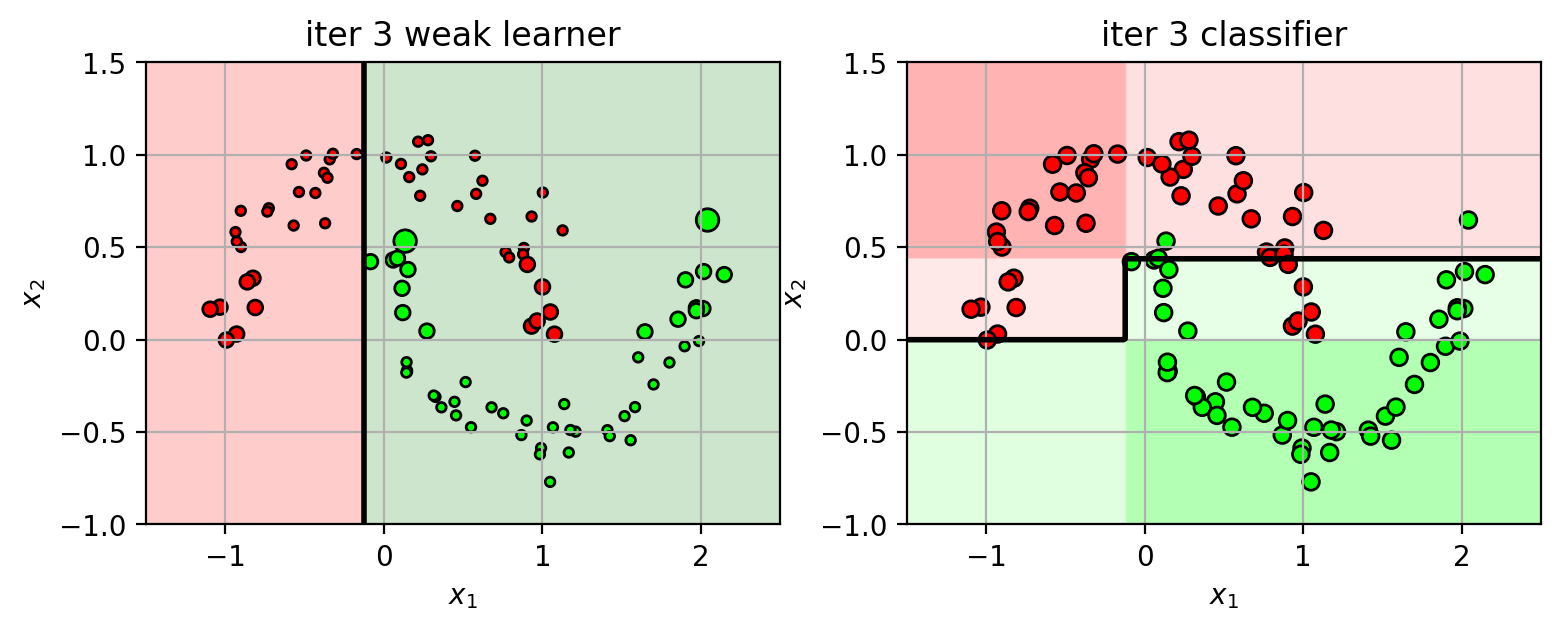
Iteration 1

  • Initially, weights for all training samples are equal: $w_i = 1/N$
    • Pick best weak learner $h_1(\mathbf{x})$.
1
plts[1]

png

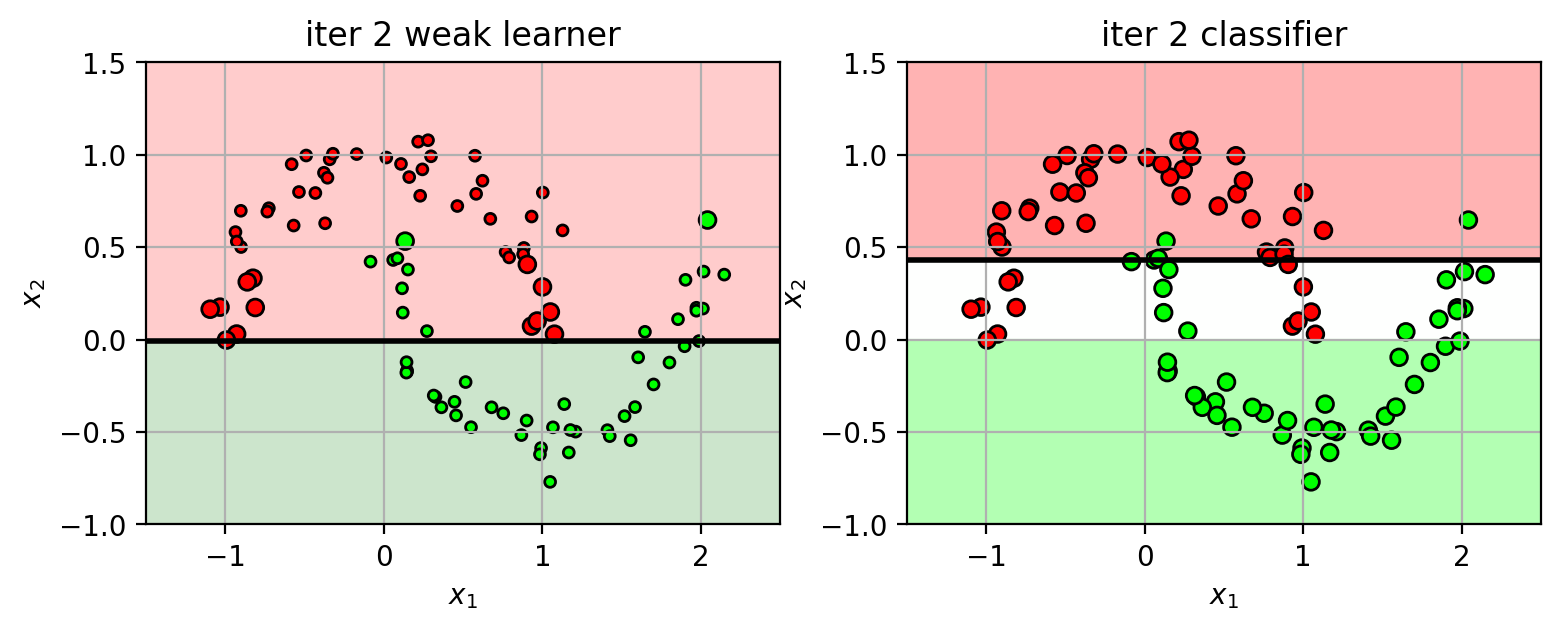
Iteration 2 (part 1)

  • points are re-weighted based on the previous errors:
    • increase weights for misclassified samples: $w_i = w_i e^{\alpha}$
    • decrease weights for correctly classified samples: $w_i = w_i e^{-\alpha}$
    • $\alpha = 0.5 \log \frac{1-err}{err}$ is based on the weighted error of the previous weak learner.
    • (larger circles indicates higher weight)
1
plts[2]

png

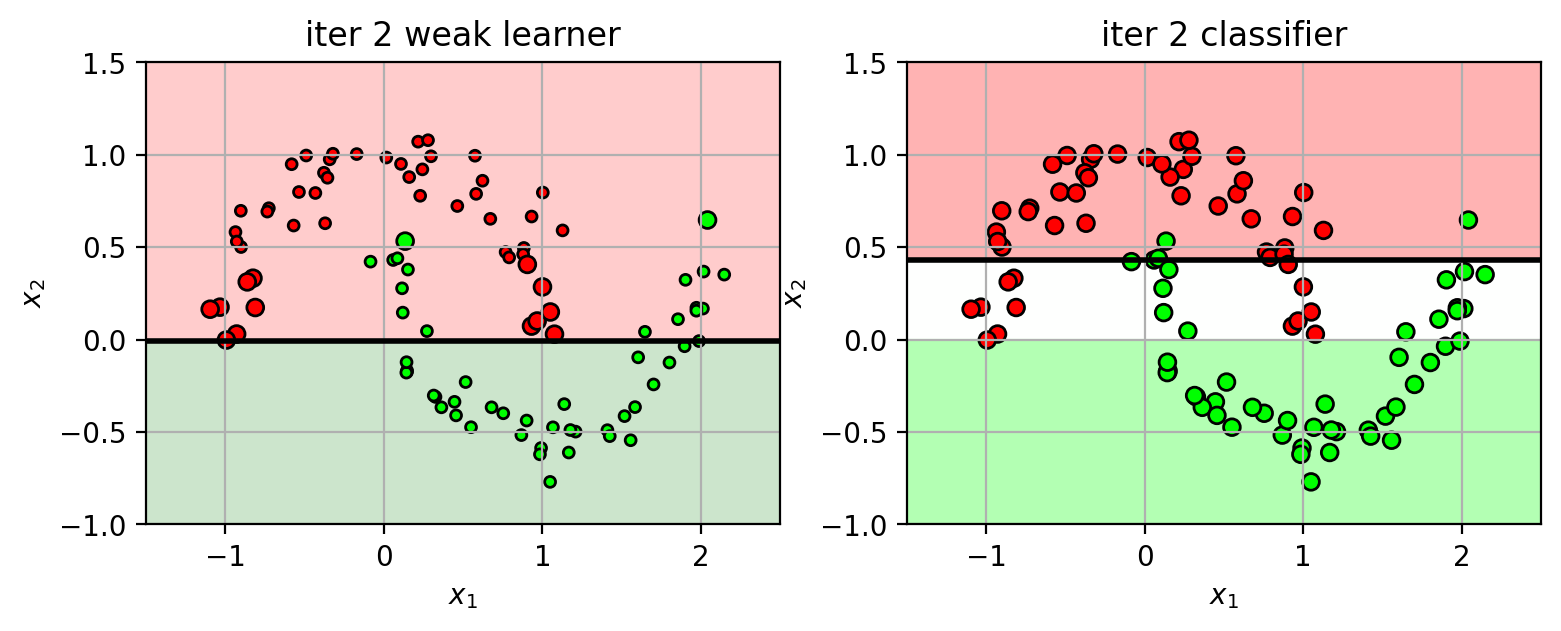
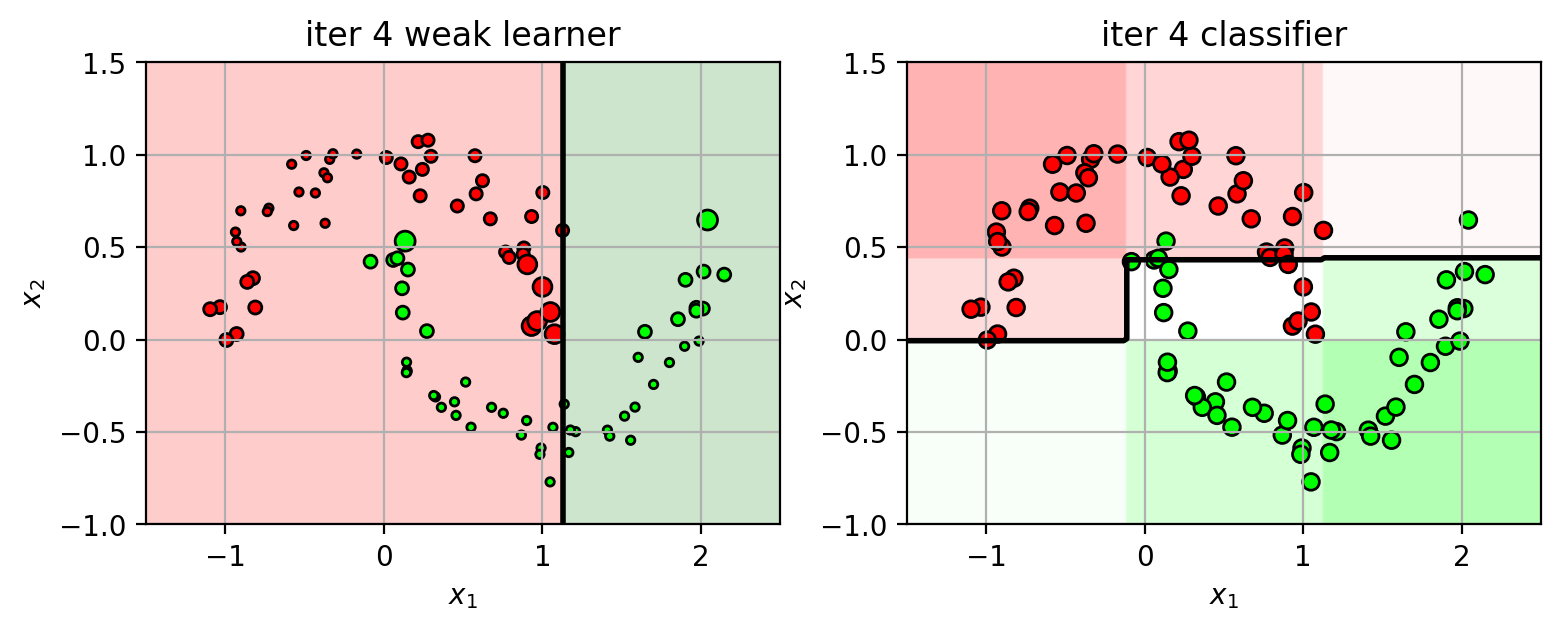
Iteration 2 (part 2)

  • using the weighted data, train another weak learner $h_2(\mathbf{x})$.
  • the classifier function is the weighted sum of weak learners
    • $f_2(\mathbf{x}) = f_1(\mathbf{x}) + \alpha_2 h_2(\mathbf{x})$
1
plts[2]

png

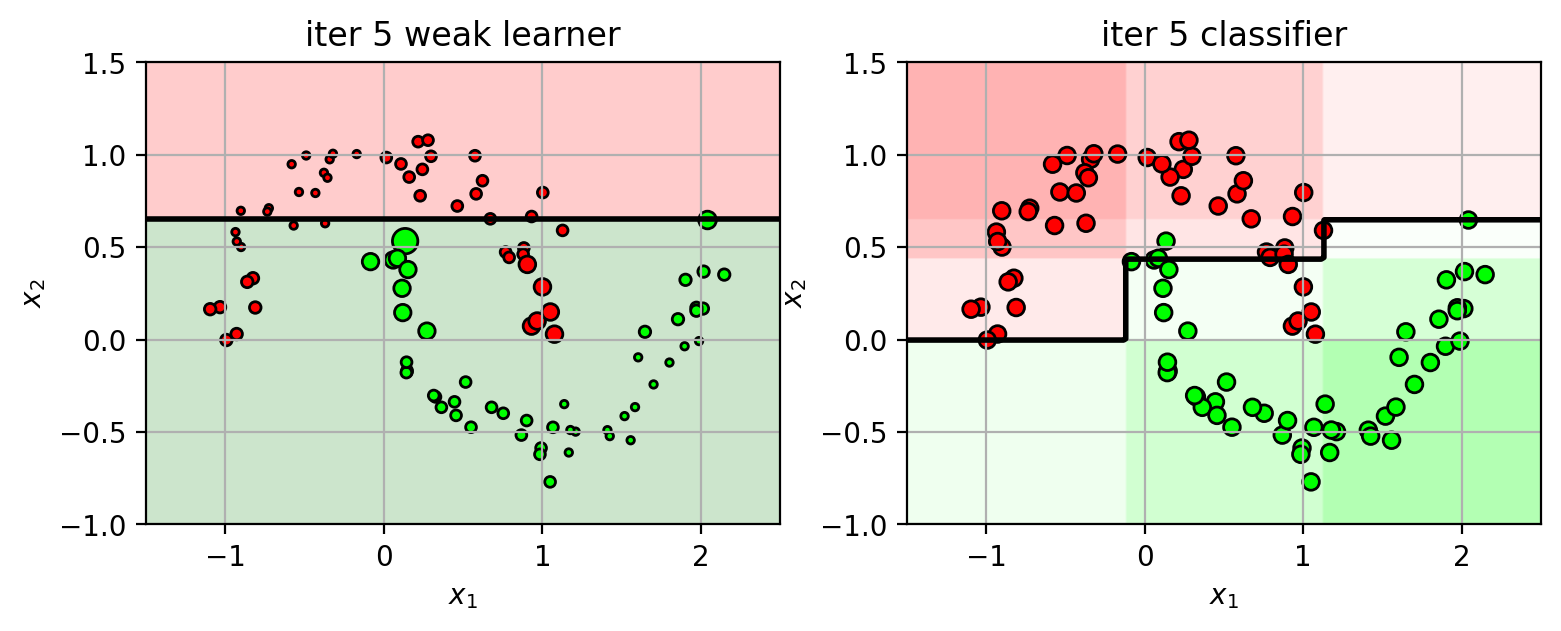
Keep iterating…

1
plts[3]

png

1
plts[4]

png

1
plts[5]

png

  • After many iterations…
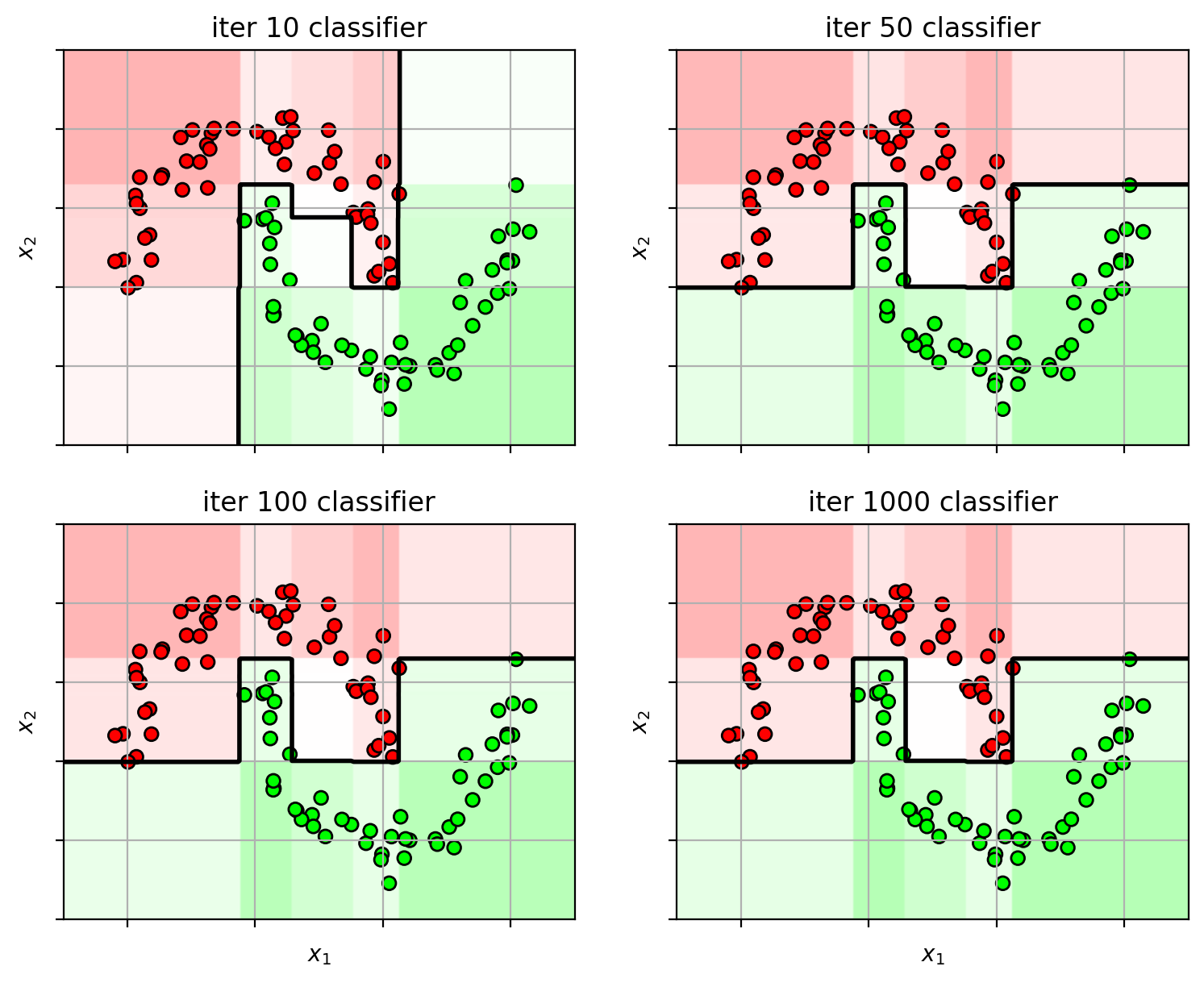
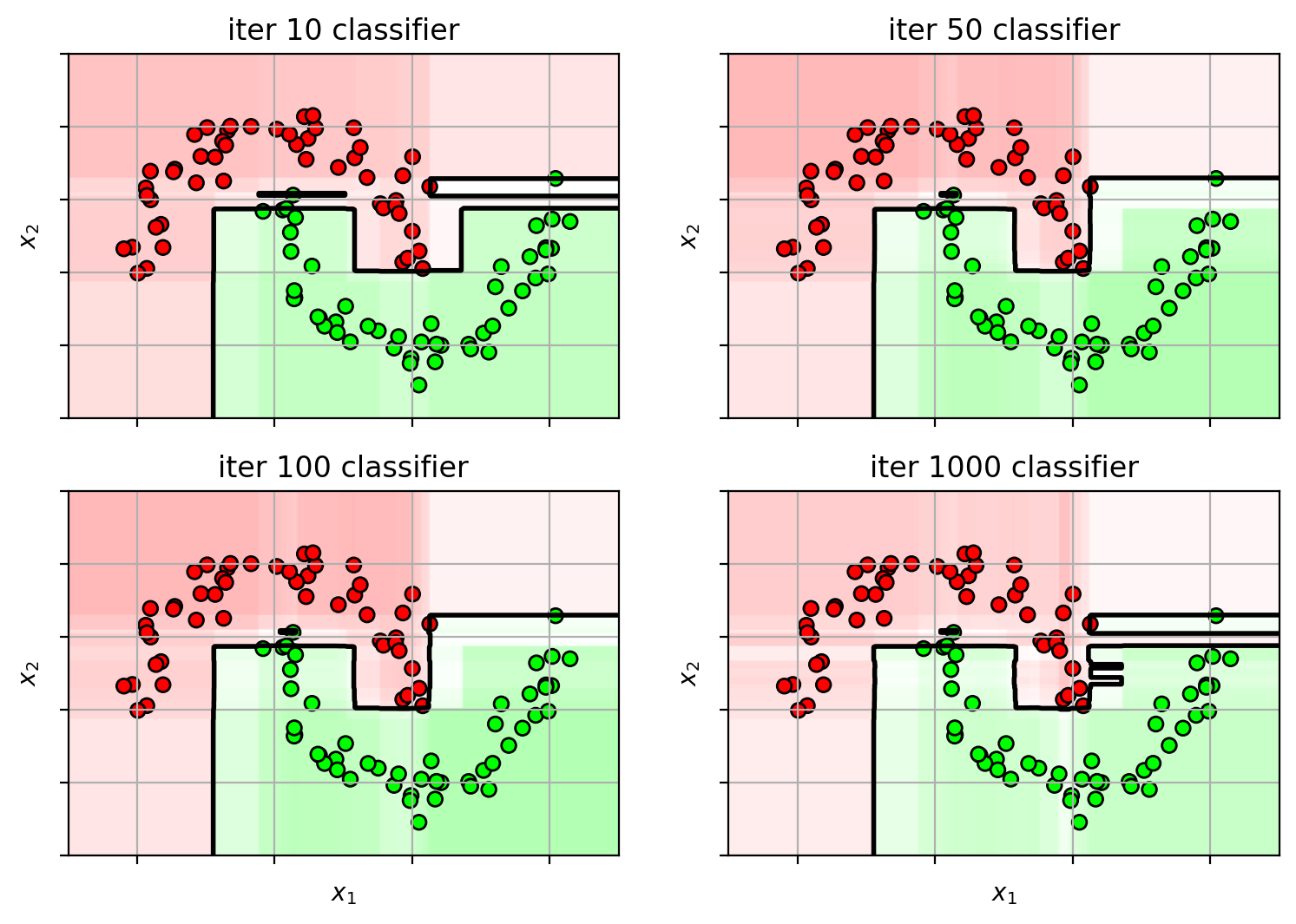
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
ns = [10, 50, 100, 1000]

adafig = plt.figure(figsize=(9,7))
for i,n in enumerate(ns):
    clf = ensemble.AdaBoostClassifier(n_estimators=n, random_state=4487)
    clf.fit(X3, Y3)
    
    plt.subplot(2,2,i+1)
    plot_boosting(clf, axbox3, X3)
    plt.scatter(X3[:,0], X3[:,1], c=Y3, cmap=mycmap, edgecolors='k')
    if i>=2:
        plt.xlabel('$x_1$')
    plt.ylabel('$x_2$')
    plt.gca().xaxis.set_ticklabels([])
    plt.gca().yaxis.set_ticklabels([])
    plt.title('iter '+str(n) + " classifier")
plt.close()
1
adafig

png

Adaboost Algorithm

  • Given data ${(\mathbf{x}_i, y_i)}$.
  • Initialize data weights, $w_i=1/N, \forall i$.
  • For $t$ = 1 to T,
    • choose weak learner $h_t(\mathbf{x})$
      • minimize the weighted classification error: $\epsilon_t = \sum_{i=1}^N w_i \mathbb{1}(h_t(\mathbf{x}_i) \neq y_i)$.
    • Set the weak learner weight: $\alpha_t = \frac{1}{2}\log(\frac{1-\epsilon_t}{\epsilon_t})$
    • Add to ensemble: $f_t(\mathbf{x}) = f_{t-1}(\mathbf{x}) + \alpha_t h_t(\mathbf{x})$.
    • Update data weights:
      • for all $\mathbf{x}_i$ misclassified, increase weight: $w_i \leftarrow w_i e^{\alpha_t}$.
      • for all $\mathbf{x}_i$ correctly classified, decrease weight: $w_i \leftarrow w_i e^{-\alpha_t}$.
      • normalize weights, so that $\sum_i w_i = 1$.

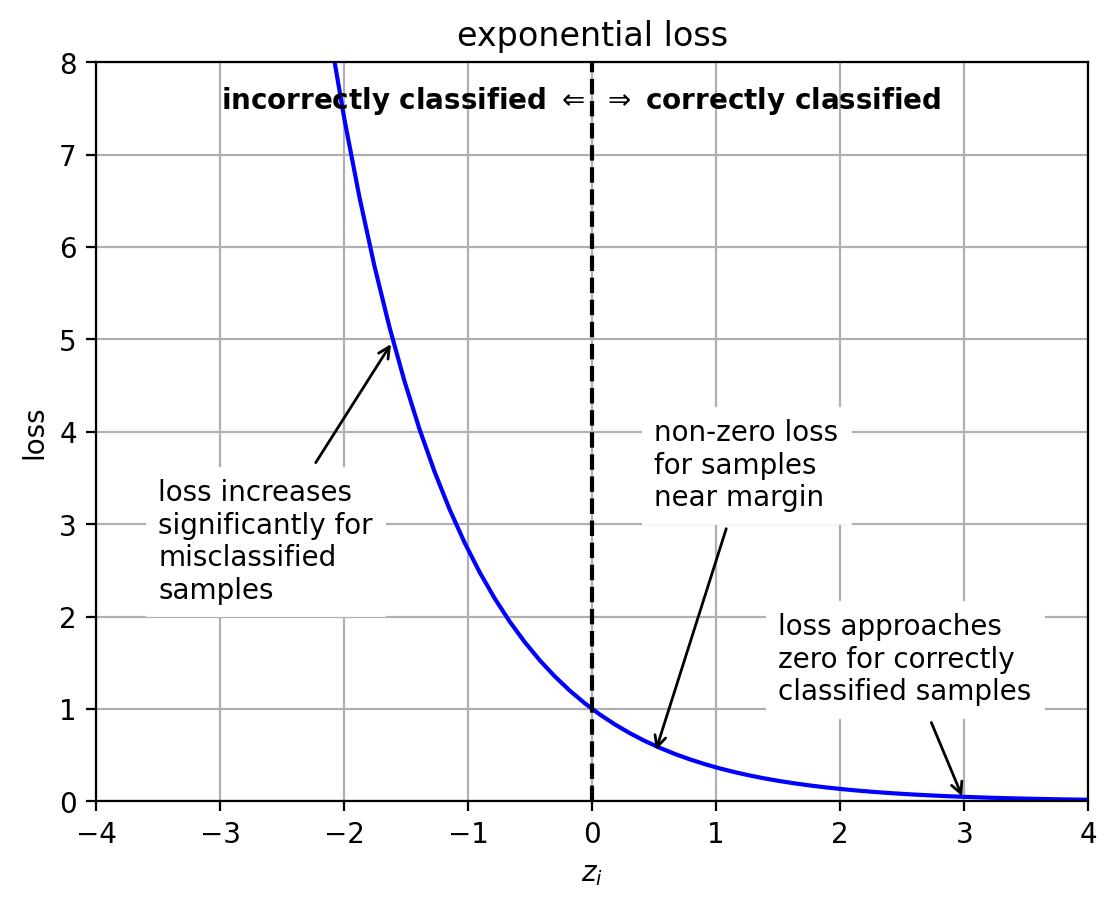
Adaboost loss function

  • It can be shown that Adaboost is minimizing:
    $$\min_f \sum_i e^{-y_i f(\mathbf{x}_i)}$$

  • Thus, it is an exponential loss function

    • $L(z_i) = e^{-z_i}$
      • $z_i = y_i f(\mathbf{x}_i)$
    • very sensitive to misclassified outliers.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
z = linspace(-6,6,100)
logloss = log(1+exp(-z))
hingeloss = maximum(0, 1-z)
exploss = exp(-z)
lossfig = plt.figure()
plt.plot(z,exploss, 'b-')

plt.plot([0,0], [0,9], 'k--')
plt.text(0,7.5, "incorrectly classified $\\Leftarrow$ ", ha='right', weight='bold')
plt.text(0,7.5, " $\Rightarrow$ correctly classified", ha='left', weight='bold')

plt.annotate(text="loss increases\nsignificantly for\nmisclassified\nsamples", 
             xy=(-1.6,5), xytext=(-3.5,2.2),backgroundcolor='white',
            arrowprops=dict(arrowstyle="->"))
plt.annotate(text="non-zero loss\nfor samples\nnear margin", 
             xy=(0.5,0.5), xytext=(0.5,3.2), backgroundcolor='white',
            arrowprops=dict(arrowstyle="->"))
plt.annotate(text="loss approaches\nzero for correctly\nclassified samples", 
             xy=(3,0.0), xytext=(1.5,1.1), backgroundcolor='white',
            arrowprops=dict(arrowstyle="->"))
plt.axis([-4, 4, 0, 8])
plt.grid(True)
plt.xlabel('$z_i$');
plt.ylabel('loss')
plt.title('exponential loss')
plt.close()
1
lossfig

png

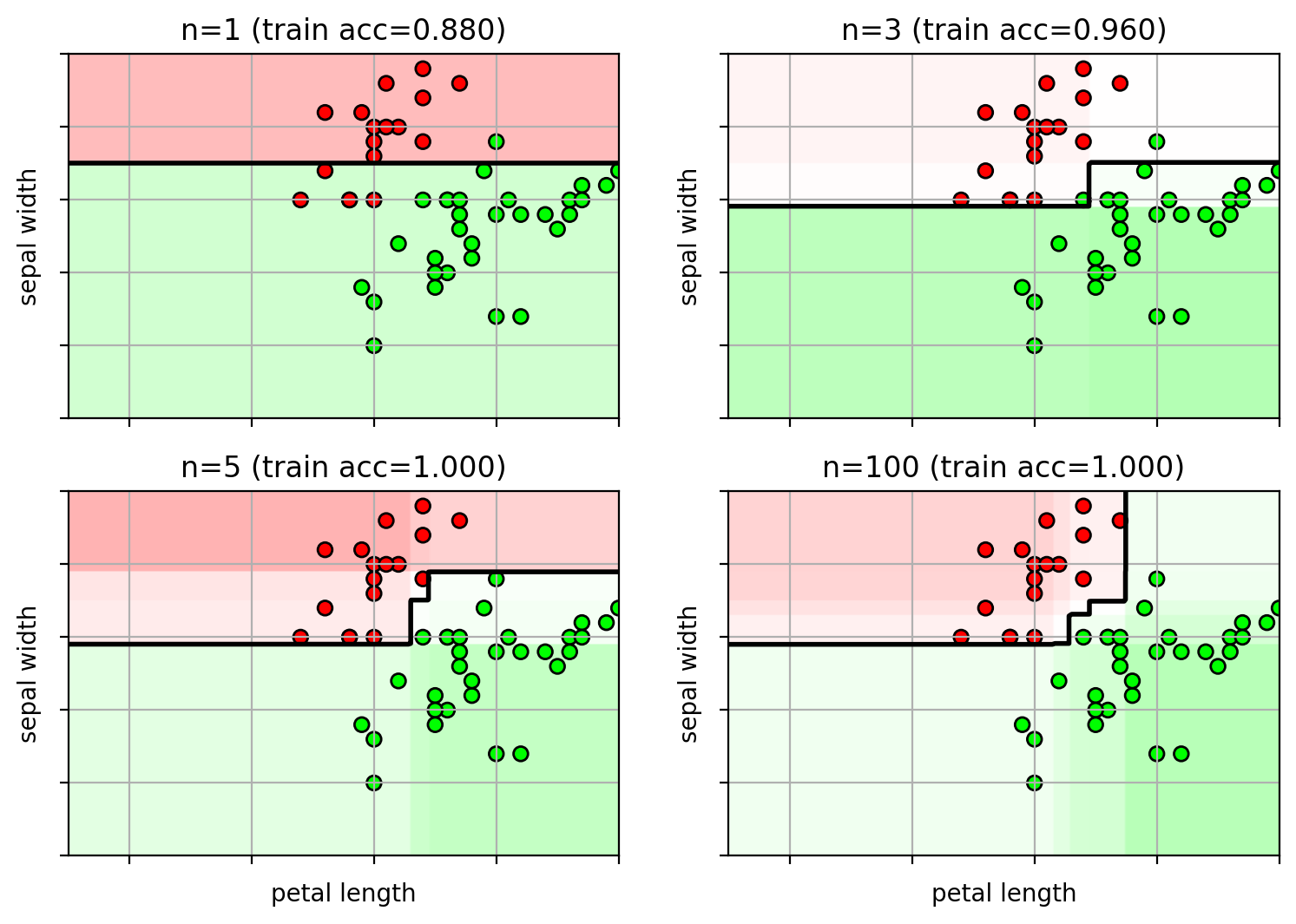
Example on Iris data

  • Too many weak-learners and AdaBoost carves out space for the outliers.
1
2
3
4
5
6
7
8
9
# load iris data each row is (petal length, sepal width, class)
from sklearn.datasets import load_iris

irisdata = load_iris()

X = irisdata.data[:100,0:2]  # the first two columns are features (petal length, sepal width)
Y = irisdata.target[:100]    # the third column is the class label (versicolor=1, virginica=2)

print(X.shape)
(100, 2)

1
2
3
4
5
6
7
8
# randomly split data into 50% train and 50% test set
from sklearn import model_selection
trainX, testX, trainY, testY = \
  model_selection.train_test_split(X, Y, 
  train_size=0.5, test_size=0.5, random_state=4487)

print(trainX.shape)
print(testX.shape)
(50, 2)
(50, 2)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
from sklearn import metrics
ns = [1, 3, 5, 100]

clf = {}
for i,n in enumerate(ns):
    clf[n] = ensemble.AdaBoostClassifier(n_estimators=n, random_state=4487)
    clf[n].fit(trainX, trainY)
    
axbox = [2.5, 7, 1.5, 4]

irisfig = plt.figure(figsize=(9,6))
for i,n in enumerate(ns):
    clfx = clf[n]
    plt.subplot(2,2,i+1)
    plot_boosting(clfx, axbox, trainX)
    plt.scatter(trainX[:,0], trainX[:,1], c=trainY, cmap=mycmap, edgecolors='k')
    if i>=2: 
        plt.xlabel('petal length')
    plt.ylabel('sepal width')
    plt.gca().xaxis.set_ticklabels([])
    plt.gca().yaxis.set_ticklabels([])
    trainerr = metrics.accuracy_score(trainY, clfx.predict(trainX))
    plt.title("n=" + str(n) + " (train acc={:.3f})".format(trainerr))
plt.close()
1
irisfig

png

  • Note: sklearn uses Real AdaBoost by default
    • uses class probabilities instead of binary class predictions (usually converges faster and has lower error)
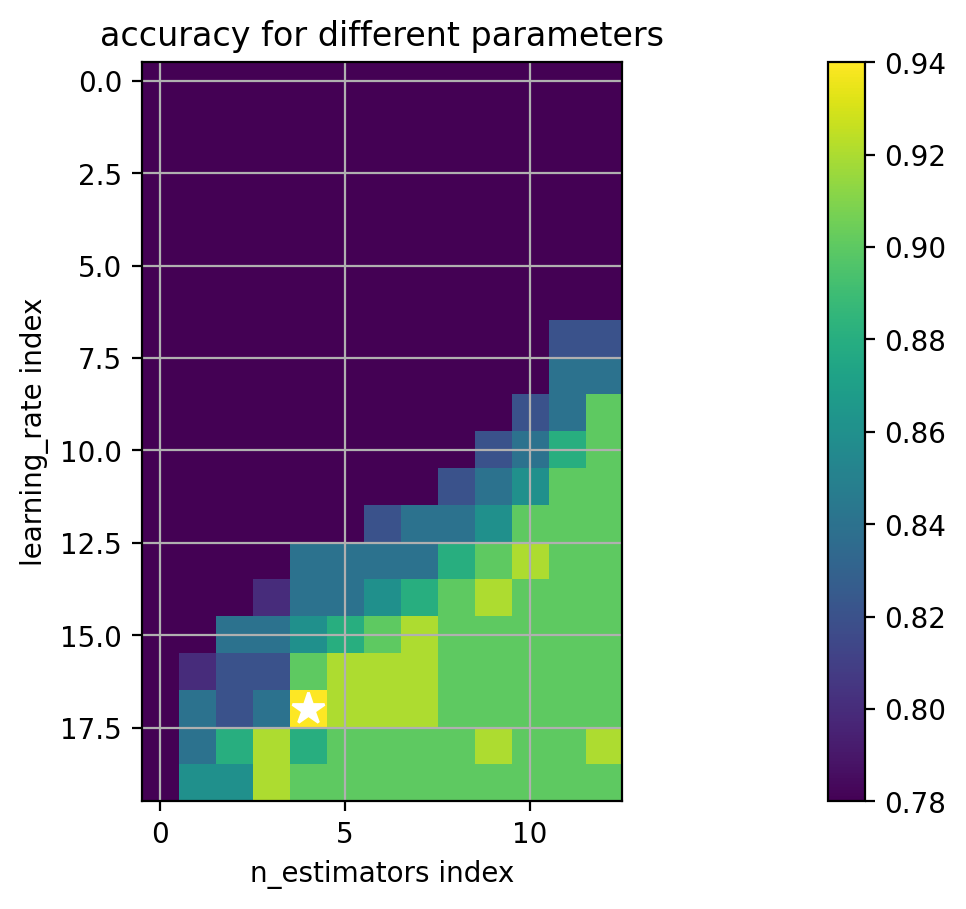
  • Two hyperparameters regularize boosting:
    1. the number of weak learners - how many boosting iterations
    2. the “learning rate” - a factor for scaling the contribution of each weak-learner
    • usually between 0 and 1.
    • Also called “shrinkage”.
  • Smaller learning rates require more weak learners.
  • Estimate with cross-validation.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
def extract_grid_scores(modelcv, paramgrid):
    "extract CV scores from GridSearchCV and put into a matrix"
    # get parameters
    pkeys = list(paramgrid.keys())
    
    # initialize empty score matrix
    scoresize = [len(paramgrid[p]) for p in pkeys]
    avgscores = zeros(scoresize)

    # fill in the matrix with run for each parameter set
    for rm,rp in zip(modelcv.cv_results_['mean_test_score'], modelcv.cv_results_['params']):
        # get the index into each of the parameter lists
        myind = [where(rp[p] == paramgrid[p]) for p in pkeys]
        avgscores[tuple(myind)] = rm    # put the score

    # location of best score
    bestind = [where(modelcv.best_params_[p] == paramgrid[p]) for p in pkeys]

    return avgscores, pkeys, bestind
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# setup the list of parameters to try
paramgrid = {'learning_rate': logspace(-6,0,20), 
             'n_estimators': array([1, 2, 3, 5, 10, 15, 20, 25, 50, 100, 200, 500, 1000])
            }
print(paramgrid)

# setup the cross-validation object
# (NOTE: using parallelization in GridSearchCV, not in AdaBoost)
adacv = model_selection.GridSearchCV(ensemble.AdaBoostClassifier(random_state=4487),
                                 paramgrid, cv=5, n_jobs=-1) # n_jobs并行运行的核数; verbose=10可以输出进度

# run cross-validation (train for each split)
adacv.fit(trainX, trainY);

print("best params:", adacv.best_params_)
{'learning_rate': array([1.00000000e-06, 2.06913808e-06, 4.28133240e-06, 8.85866790e-06,
       1.83298071e-05, 3.79269019e-05, 7.84759970e-05, 1.62377674e-04,
       3.35981829e-04, 6.95192796e-04, 1.43844989e-03, 2.97635144e-03,
       6.15848211e-03, 1.27427499e-02, 2.63665090e-02, 5.45559478e-02,
       1.12883789e-01, 2.33572147e-01, 4.83293024e-01, 1.00000000e+00]), 'n_estimators': array([   1,    2,    3,    5,   10,   15,   20,   25,   50,  100,  200,
        500, 1000])}
best params: {'learning_rate': 0.23357214690901212, 'n_estimators': 10}

1
2
3
4
5
6
7
8
9
(avgscores, pnames, bestind) = extract_grid_scores(adacv, paramgrid)
paramfig = plt.figure()
plt.imshow(avgscores, interpolation='nearest')
plt.plot(bestind[1], bestind[0], '*w', markersize=12)
plt.ylabel(pnames[0] + ' index'); plt.xlabel(pnames[1] + ' index')
plt.grid(True)
plt.title('accuracy for different parameters')
plt.colorbar()
plt.axis('image');

png

1
2
3
4
5
6
# predict from the model
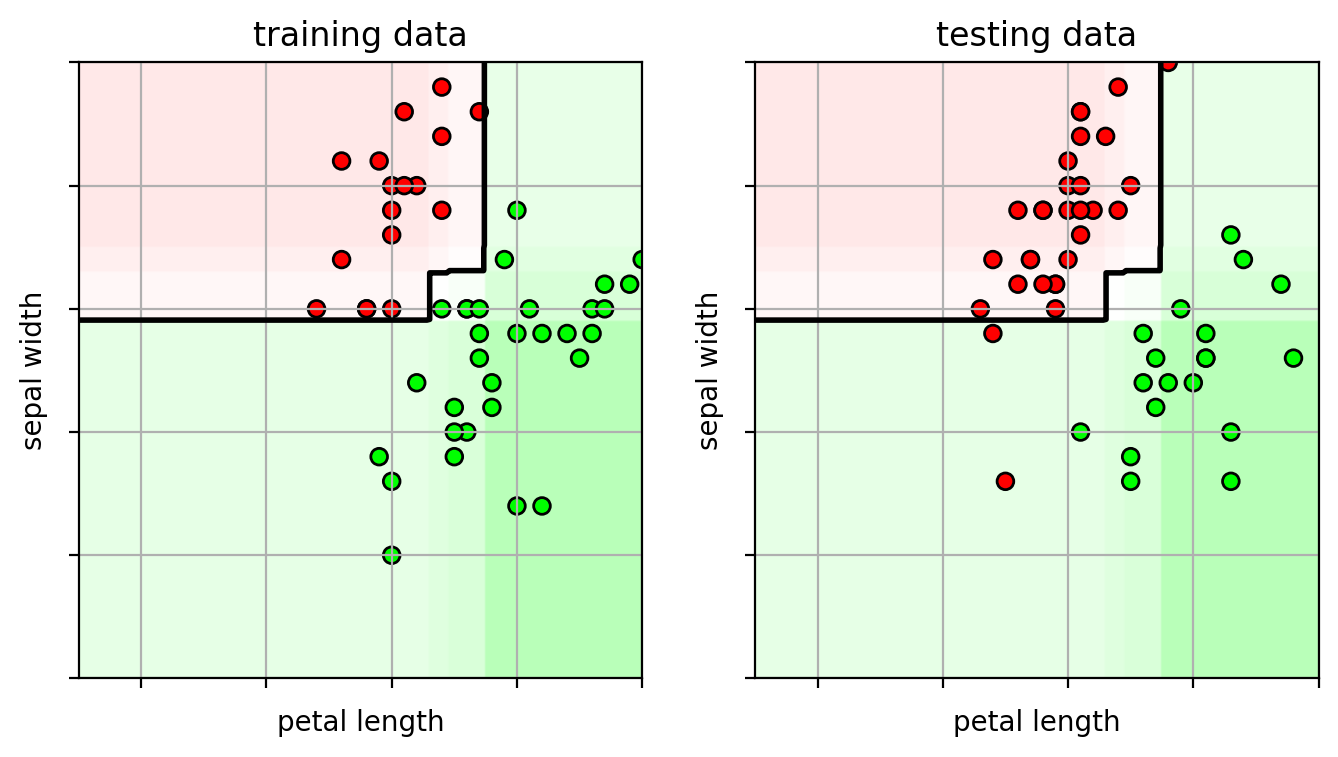
predY = adacv.predict(testX)

# calculate accuracy
acc      = metrics.accuracy_score(testY, predY)
print("test accuracy =", acc)
test accuracy = 0.94

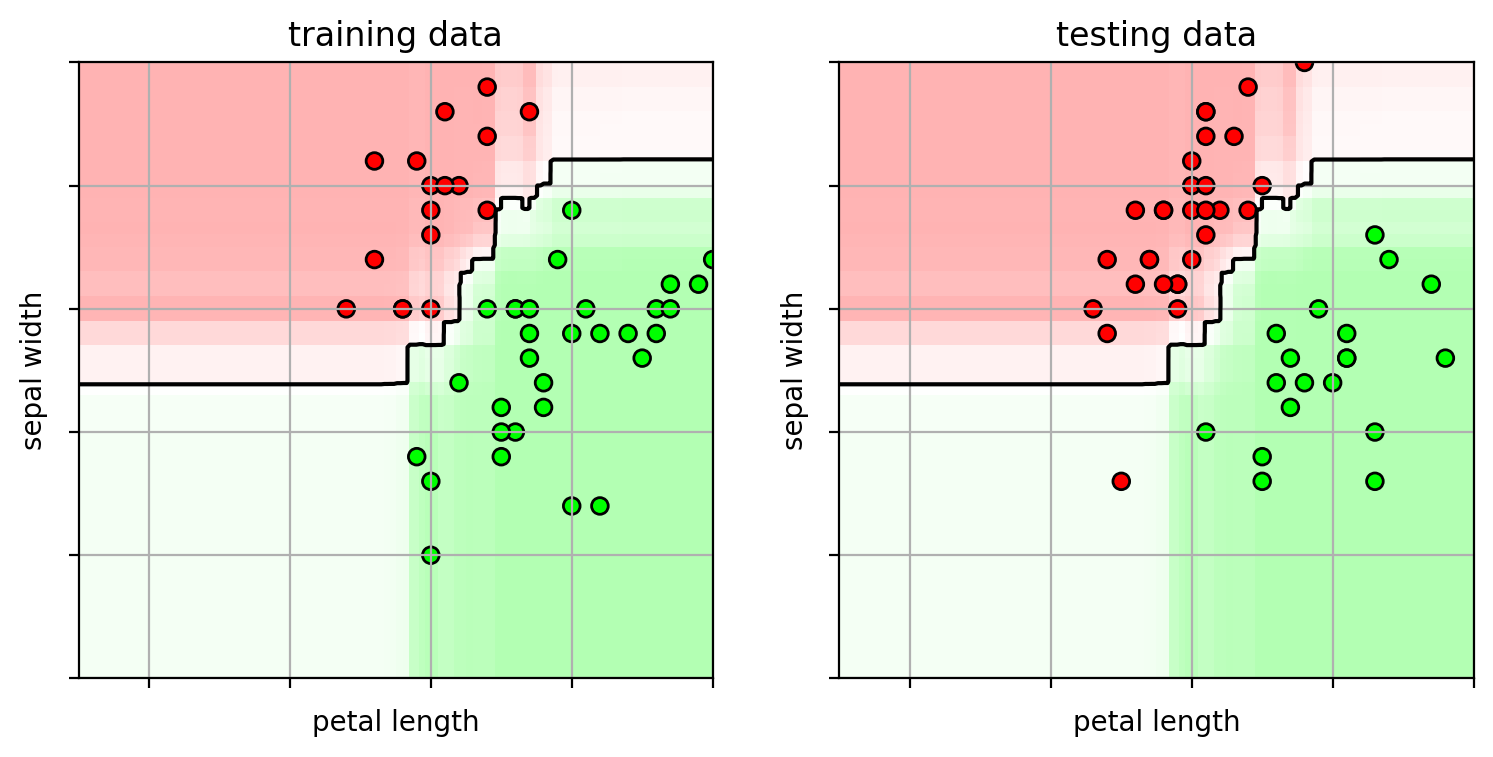
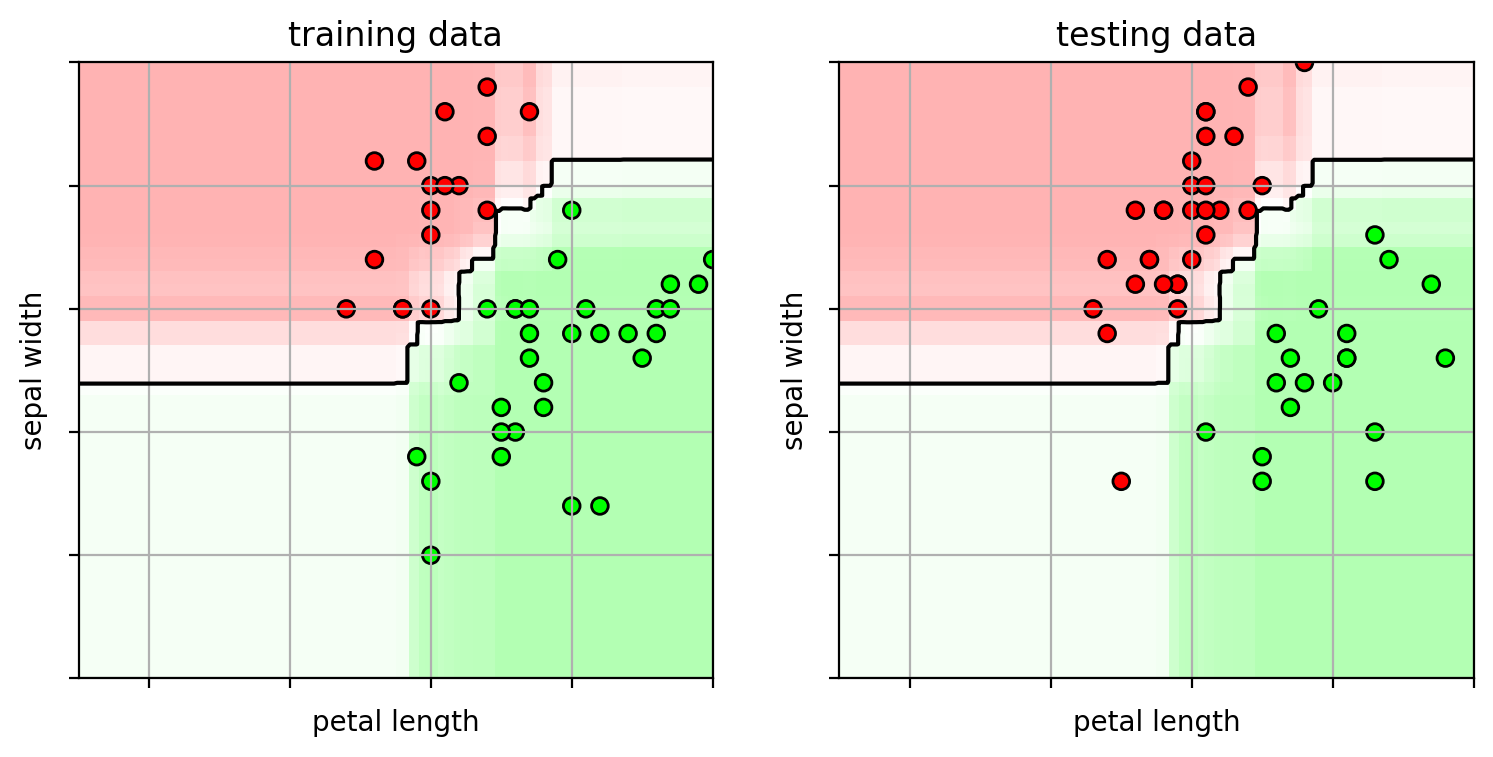
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
ifig2 = plt.figure(figsize=(8,4))
plt.subplot(1,2,1)
plot_boosting(adacv.best_estimator_, axbox, trainX)
plt.scatter(trainX[:,0], trainX[:,1], c=trainY, cmap=mycmap, edgecolors='k')
plt.xlabel('petal length'); plt.ylabel('sepal width')
plt.gca().xaxis.set_ticklabels([])
plt.gca().yaxis.set_ticklabels([])
plt.title("training data")

plt.subplot(1,2,2)
plot_boosting(adacv.best_estimator_, axbox, trainX)
plt.scatter(testX[:,0], testX[:,1], c=testY, cmap=mycmap, edgecolors='k')
plt.xlabel('petal length'); plt.ylabel('sepal width')
plt.gca().xaxis.set_ticklabels([])
plt.gca().yaxis.set_ticklabels([])
plt.title("testing data")
plt.close()
1
ifig2

png

  • Boosting can do feature selection
    • each decision stump classifier looks at one feature
  • One of the original face detection methods (Viola-Jones) used Boosting.
    • extract a lot of image features from the face
    • during training, Boosting learns which ones are the most useful.

Gradient Boosting

  • Variant of boosting

    • each iteration fits the residual between the current predictions and the true labels.
    • the residual is computed as the gradient of the loss function.

  • It’s a gradient descent algorithm

    • in each iteration, the weak learner fits the gradient of the loss
      • $h_t(\mathbf{x}) \approx \frac{dL}{d\mathbf{f}}$

  • and adds it to the function:

    • $f_t(\mathbf{x}) = f_{t-1}(\mathbf{x}) - \alpha_t h_t(\mathbf{x}) \approx f_{t-1}(\mathbf{x}) - \alpha_t \frac{dL}{d\mathbf{f}_{t-1}}$

  • Generalizes boosting to other loss functions.

  • Typically uses decision trees for the weak learner:

    • At each node, move down the tree based on that node’s criteria.
    • leaf node contains the prediction
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
import xgboost as xgb
ns = [10, 50, 100, 1000]

xgbfig = plt.figure(figsize=(9,6))
for i,n in enumerate(ns):
    clf = xgb.XGBClassifier(objective="binary:logistic", eval_metric='logloss',
                            random_state=42, n_estimators=n, use_label_encoder=False)
    clf.fit(X3, Y3)
    
    plt.subplot(2,2,i+1)
    plot_boosting(clf, axbox3, X3)
    plt.scatter(X3[:,0], X3[:,1], c=Y3, cmap=mycmap, edgecolors='k')
    if i>=2: 
        plt.xlabel('$x_1$')
    plt.ylabel('$x_2$')
    plt.gca().xaxis.set_ticklabels([])
    plt.gca().yaxis.set_ticklabels([])
    plt.title('iter '+str(n) + " classifier")
plt.close()
/Library/Frameworks/Python.framework/Versions/3.9/lib/python3.9/site-packages/xgboost/sklearn.py:1395: UserWarning: `use_label_encoder` is deprecated in 1.7.0.
  warnings.warn("`use_label_encoder` is deprecated in 1.7.0.")

Example

  • more iterations tends to overfit severely
    • because the “weak” classifier is actually strong (decision tree).
1
xgbfig

png

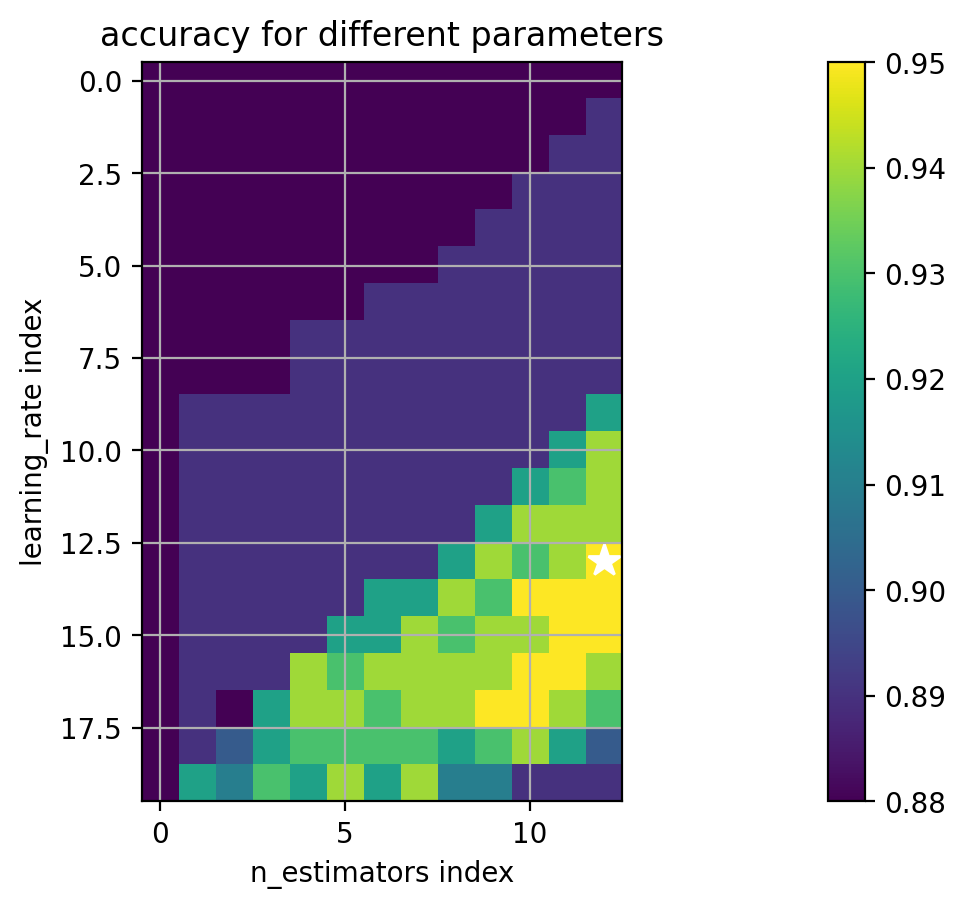
Cross-validation

  • select the best hyperparameters
    • number of estimators
    • learning rate (shrinkage term)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# use the XGBoost package, compatible with sklearn
import xgboost as xgb

# use "multi:softprob" for multi-class classification
xclf = xgb.XGBClassifier(objective="binary:logistic", eval_metric='logloss',
                         random_state=4487, use_label_encoder=False)

# setup the list of parameters to try
paramgrid = {'learning_rate': logspace(-6,0,20), 
             'n_estimators': array([1, 2, 3, 5, 10, 15, 20, 25, 50, 100, 200, 500, 1000])
            }
print(paramgrid)

# setup the cross-validation object
xgbcv = model_selection.GridSearchCV(xclf, paramgrid, cv=5, n_jobs=-1)

# run cross-validation (train for each split)
xgbcv.fit(X3, Y3);

print("best params:", xgbcv.best_params_)
{'learning_rate': array([1.00000000e-06, 2.06913808e-06, 4.28133240e-06, 8.85866790e-06,
       1.83298071e-05, 3.79269019e-05, 7.84759970e-05, 1.62377674e-04,
       3.35981829e-04, 6.95192796e-04, 1.43844989e-03, 2.97635144e-03,
       6.15848211e-03, 1.27427499e-02, 2.63665090e-02, 5.45559478e-02,
       1.12883789e-01, 2.33572147e-01, 4.83293024e-01, 1.00000000e+00]), 'n_estimators': array([   1,    2,    3,    5,   10,   15,   20,   25,   50,  100,  200,
        500, 1000])}


/Library/Frameworks/Python.framework/Versions/3.9/lib/python3.9/site-packages/xgboost/sklearn.py:1395: UserWarning: `use_label_encoder` is deprecated in 1.7.0.
  warnings.warn("`use_label_encoder` is deprecated in 1.7.0.")
/Library/Frameworks/Python.framework/Versions/3.9/lib/python3.9/site-packages/xgboost/sklearn.py:1395: UserWarning: `use_label_encoder` is deprecated in 1.7.0.
  warnings.warn("`use_label_encoder` is deprecated in 1.7.0.")


best params: {'learning_rate': 0.012742749857031322, 'n_estimators': 1000}

1
2
3
4
5
6
7
8
9
(avgscores, pnames, bestind) = extract_grid_scores(xgbcv, paramgrid)
paramfig = plt.figure()
plt.imshow(avgscores, interpolation='nearest')
plt.plot(bestind[1], bestind[0], '*w', markersize=12)
plt.ylabel(pnames[0] + ' index'); plt.xlabel(pnames[1] + ' index')
plt.grid(True)
plt.title('accuracy for different parameters')
plt.colorbar()
plt.axis('image');

png

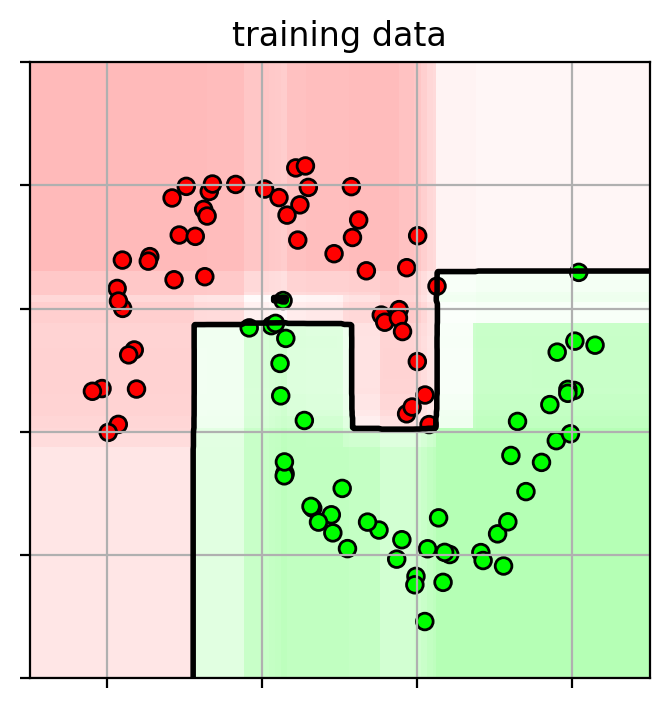
1
2
3
4
5
6
7
ifig2 = plt.figure(figsize=(4,4))
plot_boosting(xgbcv.best_estimator_, axbox3, X3)
plt.scatter(X3[:,0], X3[:,1], c=Y3, cmap=mycmap, edgecolors='k')
plt.gca().xaxis.set_ticklabels([])
plt.gca().yaxis.set_ticklabels([])
plt.title("training data")
plt.close()
1
ifig2

png

  • Since decision trees are used, there are a lot of hyperparameters to tune for the decision tree.

    • max_depth: maximum depth of the tree
    • gamma: minimum loss reduction in order to split a leaf.
    • colsample_bytree: fraction of features to randomly subsample when building a tree.
    • subsample: fraction of training data to subsample during each boosting iteration (for each tree).

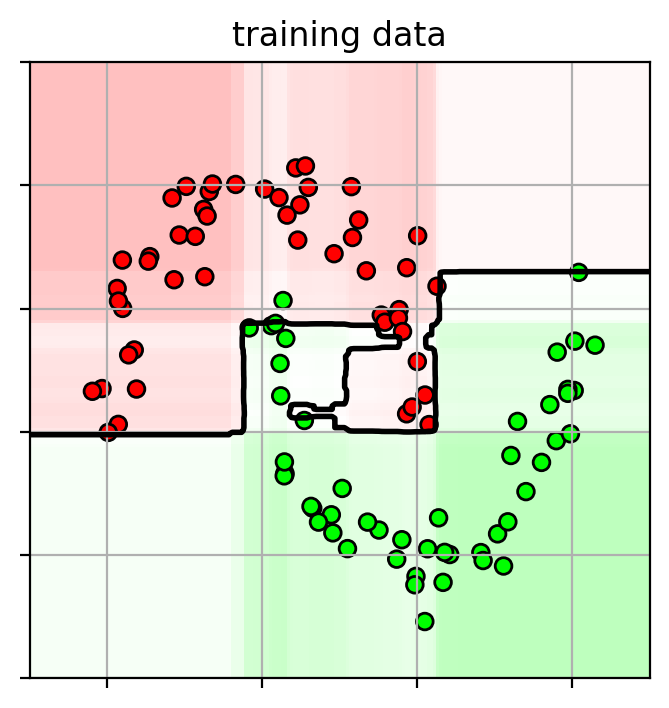
  • Problem: Too many parameters to use grid-search!

  • Solution: use randomized search

    • specify probability distributions for the parameters to try
      • stats.uniform(a, b) = uniform distribution between [a, a+b]
      • stats.randint(a,b) = random integer between [a, b]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# setup dictionary of distributions for each parameter
paramsampler = {    
    "colsample_bytree": stats.uniform(0.7, 0.3),  # default=1
    "gamma":            stats.uniform(0, 0.5),    # default=0
    "max_depth":        stats.randint(2, 6),      # default=6
    "subsample":        stats.uniform(0.6, 0.4),  # default=1
    "learning_rate":    stats.uniform(.001,1),    # default=1 (could also use loguniform)
    "n_estimators":     stats.randint(10, 1000),
}

xclf = xgb.XGBClassifier(objective="binary:logistic", eval_metric='logloss',
                         random_state=4487, use_label_encoder=False)

# cross-validation via random search
# n_iter = number of parameter combinations to try
xgbrcv = model_selection.RandomizedSearchCV(xclf, param_distributions=paramsampler, 
                            random_state=4487, n_iter=200, cv=5, 
                            verbose=1, n_jobs=-1)

xgbrcv.fit(X3, Y3)
print("best params:", xgbrcv.best_params_)
/Library/Frameworks/Python.framework/Versions/3.9/lib/python3.9/site-packages/xgboost/sklearn.py:1395: UserWarning: `use_label_encoder` is deprecated in 1.7.0.
  warnings.warn("`use_label_encoder` is deprecated in 1.7.0.")
/Library/Frameworks/Python.framework/Versions/3.9/lib/python3.9/site-packages/xgboost/sklearn.py:1395: UserWarning: `use_label_encoder` is deprecated in 1.7.0.
  warnings.warn("`use_label_encoder` is deprecated in 1.7.0.")


Fitting 5 folds for each of 200 candidates, totalling 1000 fits
best params: {'colsample_bytree': 0.9682214619643752, 'gamma': 0.43411018169657967, 'learning_rate': 0.014847933781299671, 'max_depth': 4, 'n_estimators': 152, 'subsample': 0.6743715045033899}

1
2
3
4
5
6
7
ifig2 = plt.figure(figsize=(4,4))
plot_boosting(xgbrcv.best_estimator_, axbox3, X3)
plt.scatter(X3[:,0], X3[:,1], c=Y3, cmap=mycmap, edgecolors='k')
plt.gca().xaxis.set_ticklabels([])
plt.gca().yaxis.set_ticklabels([])
plt.title("training data")
plt.close()
1
ifig2

png

Boosting Summary

  • Ensemble Classifier:

    • Combine the outputs of many “weak” classifiers to make a “strong” classifier

  • Training:

    • In each iteration,
      • training data is re-weighted based on whether it is correctly classified or not.
      • weak classifier focuses on misclassified data from previous iterations.
    • Use cross-validation to pick number of weak learners.

  • Advantages:

    • Good generalization performance
    • Built-in features selection - decision stump selects one feature at a time.

  • Disadvantages:

    • Sensitive to outliers.

Outline

  1. Nonlinear classifiers
  2. Kernel trick and kernel SVM
  3. Ensemble Methods - Boosting, Random Forests
  4. Classification Summary

Decision Tree

  • Simple “Rule-based” classifier
    • At each node, move down the tree based on that node’s criteria.
    • leaf node contains the prediction
  • Advantage: can create complex conjunction of rules
  • Disadvantage: easy to overfit by itself
    • can fix with bagging!

Random Forest Classifier

  • Use bagging to make an ensemble of Decision Tree Classifiers
    • for each Decision Tree Classifier
      • create a new training set by randomly sampling from the training set
      • for each split in a tree, select a random subset of features to use
  • for a test sample, the prediction is aggregated over all trees.
1
2
3
4
# learn a RF classifier
# use 4 trees
clf = ensemble.RandomForestClassifier(n_estimators=4, random_state=4487, n_jobs=-1)
clf.fit(X3, Y3)
RandomForestClassifier(n_estimators=4, n_jobs=-1, random_state=4487)
In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
def plot_rf(model, axbox, X):
    # grid points
    xr = [ linspace(axbox[0], axbox[1], 200), 
           linspace(axbox[2], axbox[3], 200) ]

    # make a grid for calculating the posterior, 
    #  then form into a big [N,2] matrix
    xgrid0, xgrid1 = meshgrid(xr[0], xr[1])
    allpts = c_[xgrid0.ravel(), xgrid1.ravel()]

    # calculate the decision function
    score = model.predict_proba(allpts)[:,1].reshape(xgrid0.shape)

    plt.imshow(score, origin='lower', extent=axbox, alpha=0.30, cmap=mycmap, 
               vmin=0, vmax=1, aspect='auto')

    plt.contour(xr[0], xr[1], score, levels=[0.5], linestyles='solid', colors='k')
    
    plt.axis(axbox); plt.grid(True)    
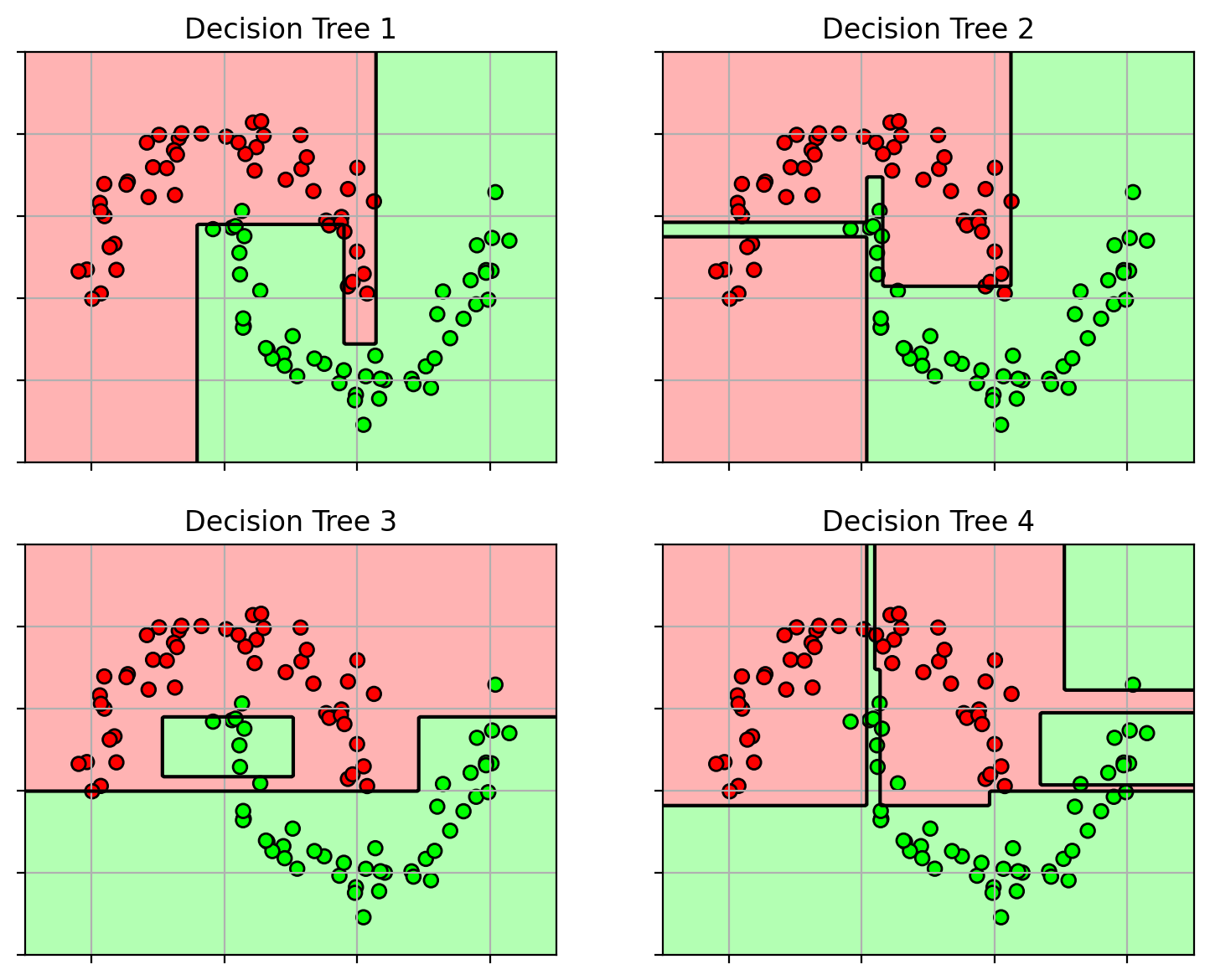
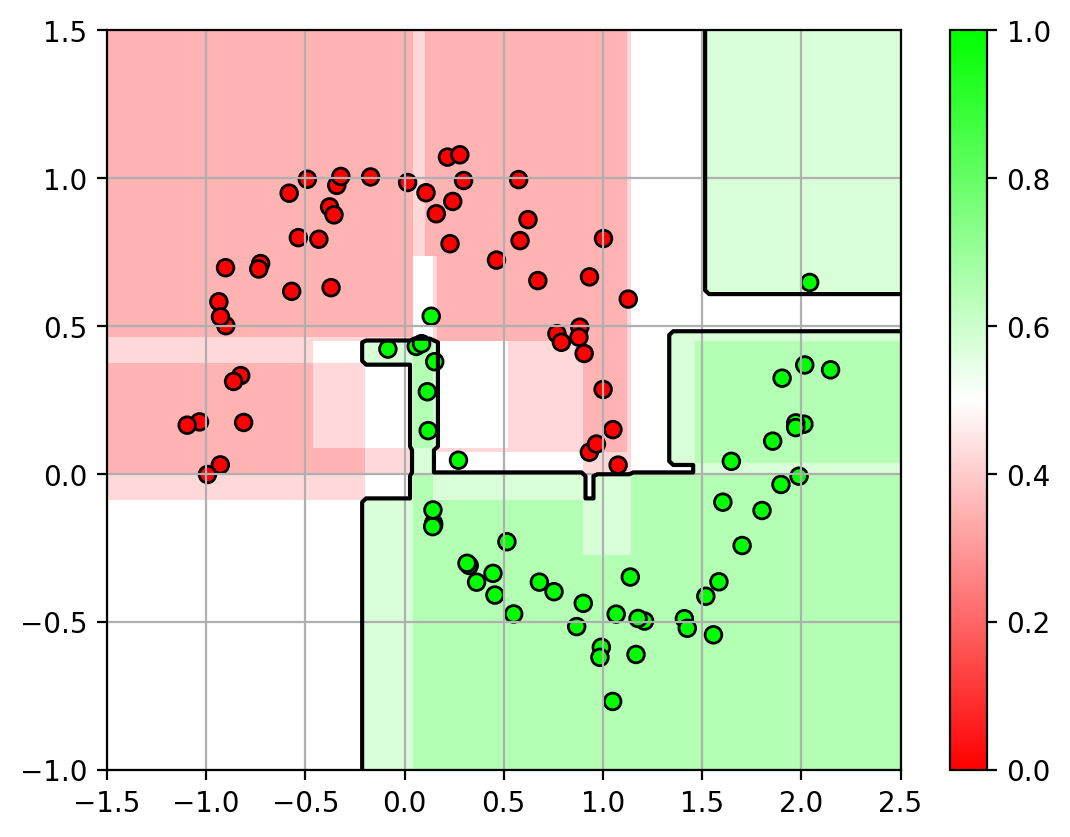
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
axbox = [-1.5, 2.5, -1, 1.5]

dtfig = plt.figure(figsize=(9,7))
for i,d in enumerate(clf.estimators_):
    plt.subplot(2,2,i+1)
    plot_rf(d, axbox, X3)
    plt.scatter(X3[:,0], X3[:,1], c=Y3, cmap=mycmap, edgecolors='k')
    plt.gca().xaxis.set_ticklabels([])
    plt.gca().yaxis.set_ticklabels([])
    plt.title("Decision Tree " + str(i+1))
plt.close()

rffig = plt.figure()
plot_rf(clf, axbox, X3)
plt.scatter(X3[:,0], X3[:,1], c=Y3, cmap=mycmap, edgecolors='k')
plt.colorbar()
plt.close()
  • Here are the 4 decision trees
    • each uses a different random sampling of original training set
1
dtfig

png

  • and the aggregated classifier
1
rffig

png

  • Using more trees
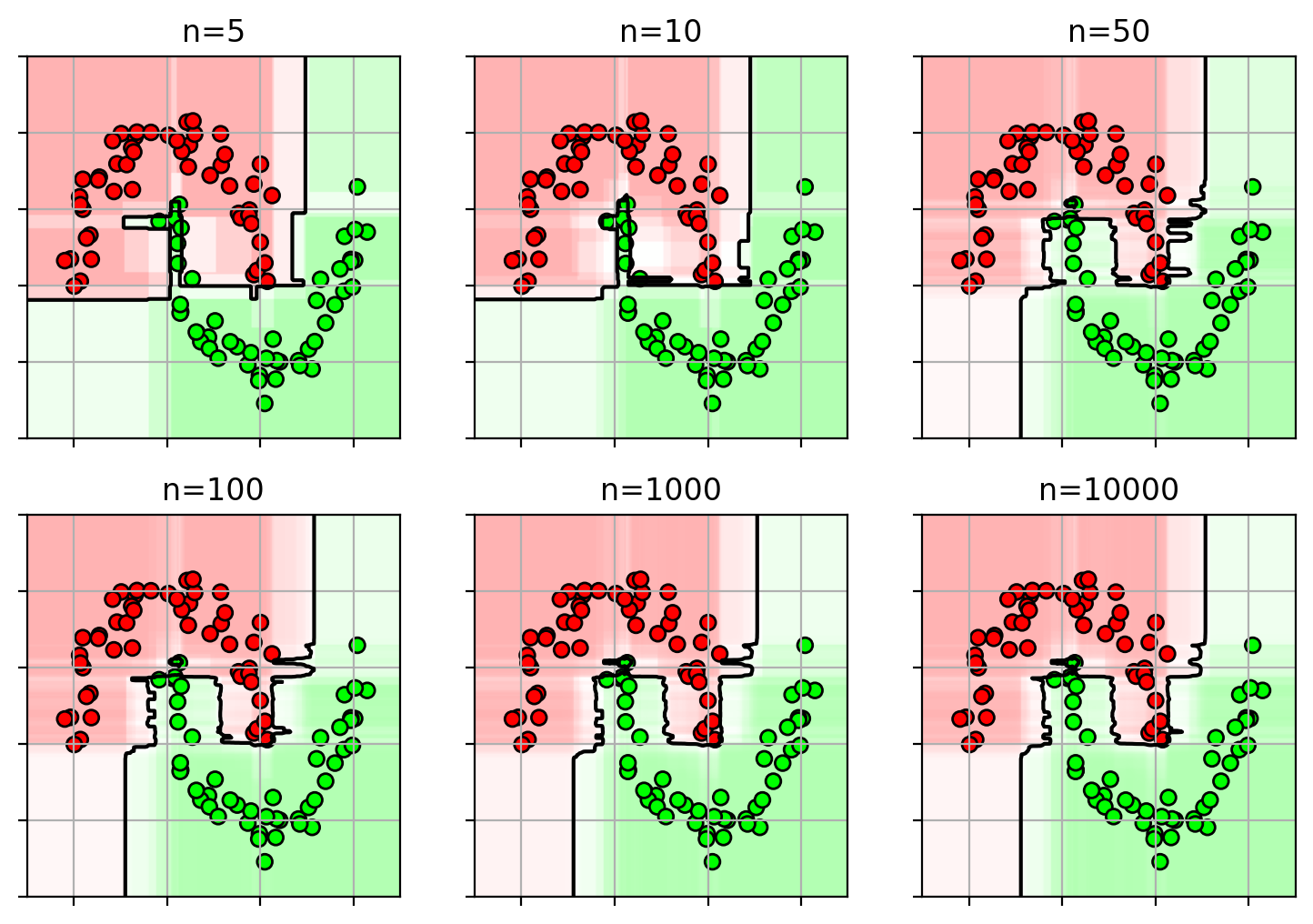
1
2
3
4
5
6
7
8
9
10
11
12
13
14
# learn RF classifiers for different n_estimators
rffig = plt.figure(figsize=(9,6))
clfs = {}
for i,n in enumerate([5, 10, 50, 100, 1000, 10000]):
    clfs[n] = ensemble.RandomForestClassifier(n_estimators=n, random_state=4487, n_jobs=-1)
    clfs[n].fit(X3, Y3)
        
    plt.subplot(2,3,i+1)
    plot_rf(clfs[n], axbox, X3)
    plt.scatter(X3[:,0], X3[:,1], c=Y3, cmap=mycmap, edgecolors='k')
    plt.gca().xaxis.set_ticklabels([])
    plt.gca().yaxis.set_ticklabels([])
    plt.title("n=" + str(n))
plt.close()
1
rffig

png

  • Try on the iris data
1
2
3
4
5
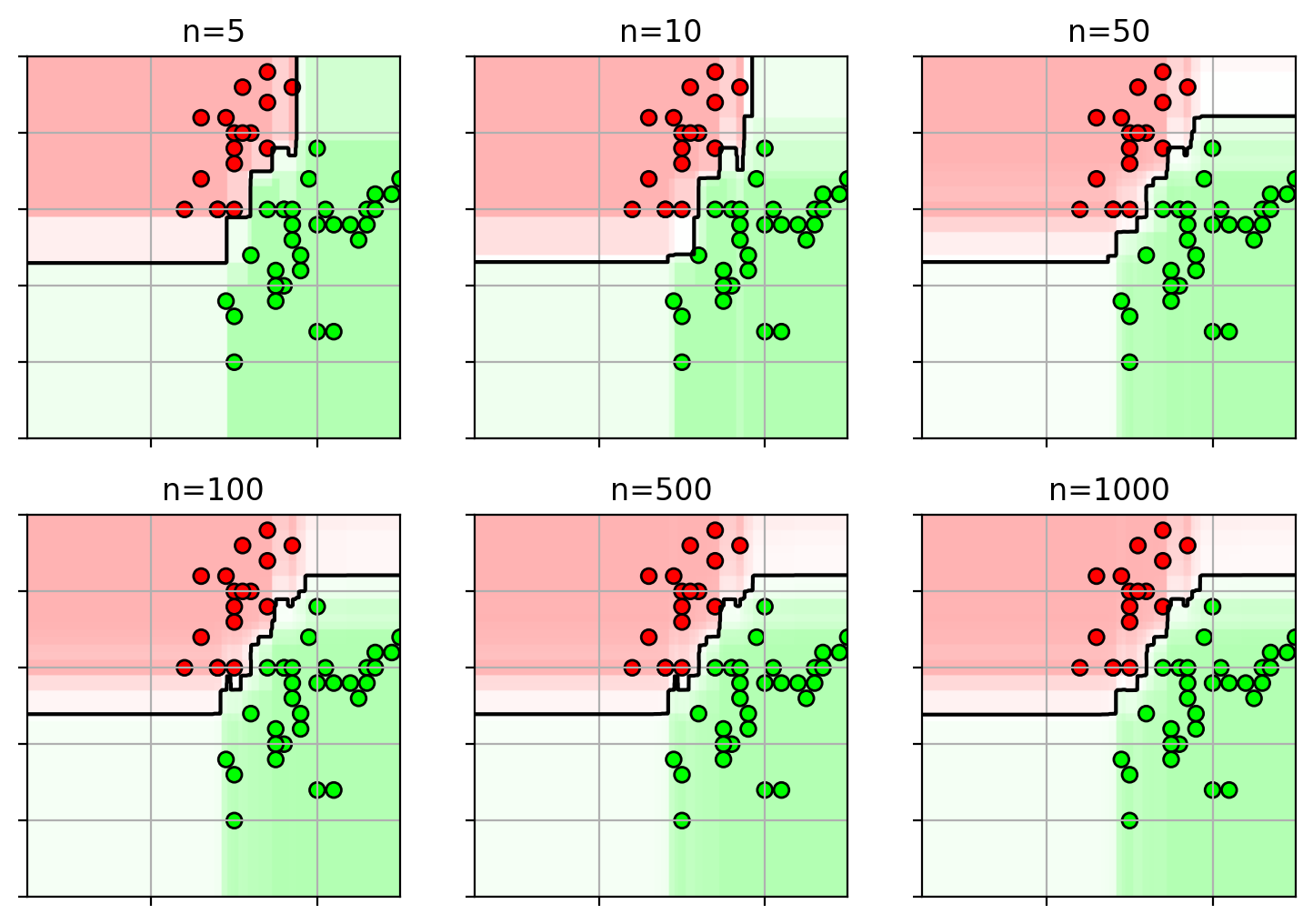
# learn RF classifiers for different n_estimators
clfs = {}
for i,n in enumerate([5, 10, 50, 100, 500, 1000]):
    clfs[n] = ensemble.RandomForestClassifier(n_estimators=n, random_state=4487, n_jobs=-1)
    clfs[n].fit(trainX, trainY)
1
2
3
4
5
6
7
8
9
10
rfnfig = plt.figure(figsize=(9,6))
axbox = [2.5, 7, 1.5, 4]
for i,n in enumerate([5, 10, 50, 100, 500, 1000]):
    plt.subplot(2,3,i+1)
    plot_rf(clfs[n], axbox, trainX)
    plt.scatter(trainX[:,0], trainX[:,1], c=trainY, cmap=mycmap, edgecolors='k')
    plt.gca().xaxis.set_ticklabels([])
    plt.gca().yaxis.set_ticklabels([])
    plt.title("n=" + str(n))
plt.close()
1
rfnfig

png

1
2
3
4
5
6
# predict from the model
predY = clfs[1000].predict(testX)

# calculate accuracy
acc      = metrics.accuracy_score(testY, predY)
print("test accuracy =", acc)
test accuracy = 0.98

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
axbox = [2.5, 7, 1.5, 4]

ifig3 = plt.figure(figsize=(9,4))
plt.subplot(1,2,1)
plot_rf(clfs[1000], axbox, trainX)
plt.scatter(trainX[:,0], trainX[:,1], c=trainY, cmap=mycmap, edgecolors='k')
plt.xlabel('petal length'); plt.ylabel('sepal width')
plt.gca().xaxis.set_ticklabels([])
plt.gca().yaxis.set_ticklabels([])
plt.title("training data")

plt.subplot(1,2,2)
plot_rf(clfs[1000], axbox, trainX)
plt.scatter(testX[:,0], testX[:,1], c=testY, cmap=mycmap, edgecolors='k')
plt.xlabel('petal length'); plt.ylabel('sepal width')
plt.gca().xaxis.set_ticklabels([])
plt.gca().yaxis.set_ticklabels([])
plt.title("testing data")
plt.close()
1
2
# classifier boundary w/ training and test data
ifig3

png

  • Important parameters for cross-validation
    • max_features - maximum number of features used for each split
    • max_depth - maximum depth of a decision tree
    • min_samples_split - minimum fraction of samples to split a node.
    • min_samples_leaf - min fraction of samples in a leaf node.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# setup the list of parameters to try
paramsampler = {#'max_features': stats.uniform(0,1.0),
                 'max_depth':         stats.randint(1,5),
                 'min_samples_split': stats.uniform(0,0.5), 
                 'min_samples_leaf':  stats.uniform(0,0.5),
               }

# setup the cross-validation object
rfrcv = model_selection.RandomizedSearchCV(
                            ensemble.RandomForestClassifier(n_estimators=100, random_state=4487, n_jobs=-1),
                            param_distributions=paramsampler, 
                            random_state=4487, n_iter=1000, cv=5, 
                            verbose=1, n_jobs=-1)

# run cross-validation (train for each split)
rfrcv.fit(trainX, trainY);

print("best params:", rfrcv.best_params_)
Fitting 5 folds for each of 1000 candidates, totalling 5000 fits
best params: {'max_depth': 4, 'min_samples_leaf': 0.013009207368046005, 'min_samples_split': 0.033821887640189785}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
axbox = [2.5, 7, 1.5, 4]

ifig3 = plt.figure(figsize=(9,4))
plt.subplot(1,2,1)
plot_rf(rfrcv.best_estimator_, axbox, trainX)
plt.scatter(trainX[:,0], trainX[:,1], c=trainY, cmap=mycmap, edgecolors='k')
plt.xlabel('petal length'); plt.ylabel('sepal width')
plt.gca().xaxis.set_ticklabels([])
plt.gca().yaxis.set_ticklabels([])
plt.title("training data")

plt.subplot(1,2,2)
plot_rf(rfrcv.best_estimator_, axbox, trainX)
plt.scatter(testX[:,0], testX[:,1], c=testY, cmap=mycmap, edgecolors='k')
plt.xlabel('petal length'); plt.ylabel('sepal width')
plt.gca().xaxis.set_ticklabels([])
plt.gca().yaxis.set_ticklabels([])
plt.title("testing data")
plt.close()
  • Result
1
ifig3

png

1
2
3
4
5
6
# predict from the model
predY = rfrcv.predict(testX)

# calculate accuracy
acc      = metrics.accuracy_score(testY, predY)
print("test accuracy =", acc)
test accuracy = 0.98

Random Forest Summary

  • Ensemble Classifier & Training:
    • aggregate predictions over several decision trees
    • trained using different subsets of data, and different subsets of features.
  • Advantages
    • non-linear decision boundary.
    • can do feature selection.
    • good generalization.
    • fast.
  • Disadvantages
    • can be sensitive to outliers
    • based on trees – cannot well represent “diagonal” decision boundaries.