Numpy基础 | hhgw's blog

<基础向>整理自讲义

矩阵类库numpy 的方法

Zeros，生成元素为0的矩阵

B=np.zeros((2,3)) # 给定元组

ones生成元素为1 的矩阵

x=np.ones((2,3))

eye生成单位矩阵

X=np.eye(5)

生成一个5*5的单位阵

np.random.standard_normal((n,m))

生成n行m列，服从正太分布的随机数矩阵

如：

x=np.random.standard_normal((4,4))

np.random.random() 产生0~1随机数

np.random.random(n) 产生n个0~1随机数

np.random.random((n,m)) 产生n*m个0~1随机数,二维数组形式

np.random.choice(a,size=n)，从数组a中随机采n个样本

文件与矩阵

读文件到矩阵

Z=np.loadtxt (“c:\python33\S-093790.txt”)

Z就是一个矩阵；默认文件中列以空格间隔

矩阵的格式化文件保存

np.savetxt(fname, X, fmt=’格式串’, delimiter=’\t’, newline=’\r\n’)

·fname为文件名，如 c:\abc.txt

·X输出矩阵

·fmt为数据格式，如 %10.3f

·delimiter是列分隔符

·newline为换行符，一般使用\r\n。

下面语句将矩阵y保存到磁盘文件111.txt中。数据格式为宽度5位，保留2位小数。

np.savetxt(“d:\111.txt”,y,fmt=’%5.2f’, delimiter=’\t’, newline=’\r\n’)

import numpy as np

x=np.random.standard_normal((4,4))

np.savetxt(“d:\111.txt”,x,fmt=’%5.2f’, delimiter=’\t’, newline=’\r\n’)

# 偷懒写法

np.savetxt(“d:\111.txt”,x,fmt=’%5.2f’) # 默认空格间隔，换行

矩阵转置

转置：B =A.T

import numpy as np

x=np.random.standard_normal((4,4))

np.savetxt(“d:\111.txt”,x,fmt=’%5.2f’, delimiter=’\t’, newline=’\r\n’)

xt=x.T

np.savetxt(“d:\222.txt”,xt,fmt=’%5.2f’, delimiter=’\t’, newline=’\r\n’)

矩阵的 +, - , *，/, dot乘运算：

矩阵的+，-, *, / 运算：维数相同的2个矩阵，对应元素进行计算。

C=A+B 或 D=A-B

dot乘：线性代数乘：C=A.dot(B) 或 C=np.dot(A,B)或 C=A @ B

矩阵逆

逆：B=np.linalg .inv (A)

import numpy as np

x=np.random.standard_normal((4,4))

xinv=np.linalg.inv(x)

I=x @ xinv

矩阵乘方运算

矩阵每个元素的乘方，形成新矩阵

A=np.array([[1,-1,0],[2,0,-2.0]])

B=A**2

array([[1., 1., 0.],

[4., 0., 4.]])

矩阵的行和列数

size = A.shape

size[0]是行数，size[1]是列数

两矩阵合并

np.r_[ ]是行合并

np.c_[ ] 列合并

A=np.ones((3,3))

B=np.zeros((2,3))

np.r_[A,B]

array([[1., 1., 1.],

[1., 1., 1.],

[1., 1., 1.],

[0., 0., 0.],

[0., 0., 0.]])

注意：

A=np.ones(3)

B=np.zeros((2,3))

因为1维向量被看作是竖起来的，所以无法与B矩阵np.r_[ ]

np.r_[A,B] 报错，数据维度不一致

矩阵分片

x=np.random.standard_normal((4,4))

x

array([[ 1.098, -0.594, -1.353, 1.181],

[-0.686, -0.794, 1.686, -0.676],

[ 0.363, 0.419, 0.561, 1.086],

[ 0.774, -2.578, -0.436, 0.837]])

y=x[: , :2]

第一个:，代表所有行，第二个:，后跟数字2，取前两列

array([[ 1.098, -0.594],

[-0.686, -0.794],

[ 0.363, 0.419],

[ 0.774, -2.578]])

矩阵分片—指定行列索引选择

import numpy as np

a=np.random.standard_normal((9,4))

print(a)

xSel=[0,5,7]

ySel=[1,3]

b=a[xSel] # 选择指定行

b=b[:,ySel] # 再选择指定列

print(b)

b=a[xSel，ySel] # 可否？

b=a[[0,5],[1,3]]

代表[0,1],[5,3]两个位置的数字

数据过滤

给定一维数组y，y==值1, 返回元素值为True和False的一维数组，元素值等于值1的元素，返回True

import numpy as np

y=np.array([1,-1,1])

z=y==1

z值： array([ True, False, True])

长度与矩阵的行(列数)数相等且每个元素的取值为True/False 的一维数组，将其作为矩阵的行或列，可以过滤数据

y[z],取值 array([1, 1])

已知X存储了8朵鸢尾花的花瓣长、宽数据。y存储了8朵花的归属，1是山鸢尾，-1是变色鸢尾。

写语句，将X中的山鸢尾数据提取出来。

import numpy as np
X=np.array([[5.1, 3.5 ],  [4.9, 3. ],
    [5.5, 2.6 ],  [6.1, 3.0],    
    [4.7, 3.2], [4.6, 3.1],
    [5.8, 2.6], [5. , 2.3]])
y=np.array([-1, -1, 1, 1,  -1, -1,1, 1])

mask=y==1
print(X[mask])

矩阵函数

如sum（元素和）、 std（标准偏差），mean(均值)
默认情况下，这些函数对矩阵所有元素进行
由于矩阵具有行、列属性，因此，通过特别指定，这些函数也可以按行或列操作。
指定该操作的参数为axis，当axis=0时，求列方向，axis=1时，求行方向

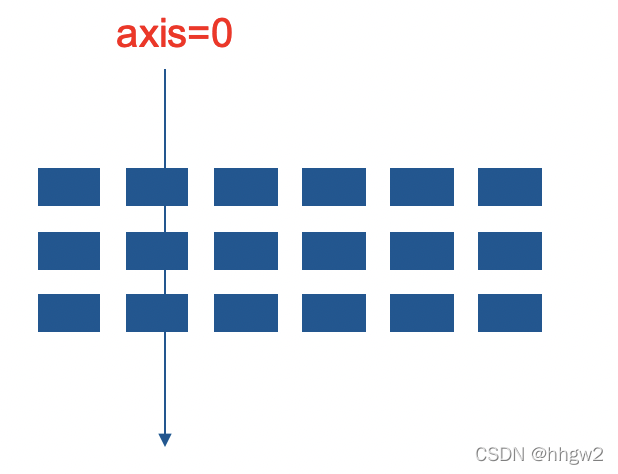
>>> x=np.array([[1,2,3],[5,6,7]])

>>> x.sum()

24

>>> x.sum(axis=0)

array([ 6, 8, 10])

>>> x.sum(axis=1)

array([ 6, 18])

矩阵与标量的运算

矩阵与标量（一个数值）运算，+、-、*、/，在每个元素上进行

zz=np.eye(3,3)

array([[ 1., 0., 0.],

[ 0., 1., 0.],

[ 0., 0., 1.]])

zz+1

array([[ 2., 1., 1.],

[ 1., 2., 1.],

[ 1., 1., 2.]])

矩阵与向量的+ - * / 扩展

+、-、*、/，指定运算在列上进行

（行运算可以转置）

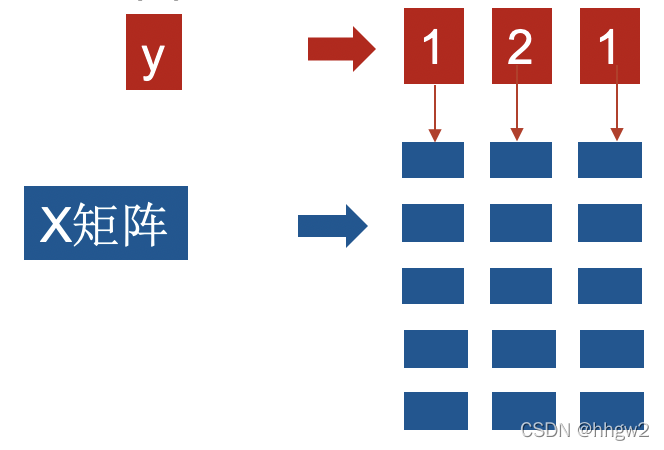
import numpy as np

X=np.random.random((5,3))

y=np.array([1,2,1])

z=X+y

print(z)

[[0.01569532 0.7719744 0.68876164]
[0.94614404 0.09550832 0.72591569]
[0.04651266 0.35518092 0.78006742]
[0.79136464 0.14264937 0.38290291]
[0.91792254 0.82318107 0.96811695]]
[[1.01569532 2.7719744 1.68876164]
[1.94614404 2.09550832 1.72591569]
[1.04651266 2.35518092 1.78006742]
[1.79136464 2.14264937 1.38290291]
[1.91792254 2.82318107 1.96811695]]

矩阵间的*、/ VS 线性代数乘

import numpy as np
x=np.array([[1,2],[3,4]])
y=np.array([[0,1],[1,2]])
z=x @ y 
print(z)
[[2  5]
 [4 11]]
dot线性代数乘
import numpy as np
x=np.array([[1,2],[3,4]])
y=np.array([[0,1],[1,2]])
z=x * y
print(z)
[[0 2]
 [3 8]]
对应元素相乘

额外内容：

矩阵Sigular Value Decomposition分解（SVD）

实矩阵的SVD分解：按特征值由大到小，逐个提取特征向量分解

B = np.linalg.svd(A)

常用于主特征提取，降维，数据可视化

实矩阵的SVD分解，将一个实矩阵分解为三个矩阵的乘积，其结果可以表达为：

A=USV

其中S为一维矩阵，其每个元素是矩阵的A的实奇异值（特征值开根号），从大到小排列

U是列正交矩阵，且每个列的模为1（所有元素的平方和开根号）

V是行正交矩阵

所谓列（行）正交，是指矩阵的任意两列（行）的对应元素的乘积之和为0

A=np.array([[1,5.0,3.0],[2.1,2.0,7.0]])
Z=np.linalg.svd(A)
Z[0]
array([[-0.58281835, -0.81260247],
       [-0.81260247,  0.58281835]])
>>> Z[1]
array([ 9.00833663,  3.35557316])
>>> Z[2]
array([[-0.25412944, -0.50389954, -0.82553224],
       [ 0.12257699, -0.86345179,  0.48931164]])

SVD分解，特征值从大到小排列

当对应最后一种物质的信号特征值，与后面一个对应噪声的特征值，比值会出现突跃

import numpy as np
A=np.loadtxt (“某数据集")
B = np.linalg.svd(A)
lamda=B[1]
for i in range(len(lamda)-1):
    print(lamda[i]/lamda[i+1])

2.041 2.309 27.370 1.226 1.096 1.088 1.031 1.018

1.040 1.130 1.060 1.062 1.020 1.078 1.047 1.135

……

所以体系中有3中组分，即体系中，只有3个特征值对应有效信号，其余为噪声